여인권 교수님의 KMOOC 강의 <통계학의 이해 2>를 수강하면서 공부한 내용을 정리해보았습니다.
잔차검진 - Residual Diagnositics
분석에 사용된 회귀모형의 적절성과 통계적 추론의 가정을 만족하는지를 확인하는 방법에 대해 알아보겠습니다.
1. 오차항의 가정

오차항에서는 세 가지가 가정되어야 합니다.
(1) 정규성
중심축량이 자유도가 n-2인 t분포를 따른다고 유도할 때 데이터가 정규분포를 만족한다고 가정하에 t분포를 유도합니다.
(2) 등분산성
MSE는 모든 분산이 동일하다는 가정하에 유도합니다.
회귀분석과 분산분석에서 제일 중요한 것은 등분산성입니다.
(3) 독립성
Y들이 선형 결합인 상태에서 분산을 유도하는데 이때 Y가 독립이라고 가정합니다.
이 세가지를 가정되어야 회귀분석을 할 수 있습니다.
잔차가 오차항의 가정을 심각하게 위반하면 통계적 추론에 문제가 발생합니다.
t분포, F검정, MSE가 성립하지 않게 됩니다.
2. 잔차 - residual
잔차는 관측값과 예측값의 차이를 의미합니다.
이론 값을 도출할 때는 확률변수 Y를 이용합니다.
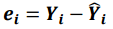
실제 분석을 할 때는 관측값 y를 이용합니다.

잔차가 특정한 패턴을 가진다면 모형(설명되는 부분)에 추가해야 할 요소가 남아 있음을 의미합니다.
따라서 잔차는 특정한 패턴이 없어야 합니다.
잔차가 오차항의 가정을 심각하게 위반하면 통계적 추론에 문제가 발생합니다.
3. 잔차그림 - Residual plot
$\hat{y}$, e의 산점도를 나타낸 것입니다.
잔차그림을 확인하면 시각적으로 등분산성을 파악할 수 있습니다.
(1) 정상적인 잔차그림
등분산성을 만족하는 잔차그림입니다.

정상적인 잔차그림은 0을 중심으로 $\hat{y}$ 값에 관계없이 일정 범위 내에서 특정한 패턴을 가지지 않게 분포됩니다.
(2) 대표적인 비정상적 잔차 그림
잔차그림을 통해 어떤 문제가 있는지 시각적으로 확인하고 해결방법을 찾을 수 있습니다.
a. $\hat{y}$가 커지면서 e의 폭이 커짐
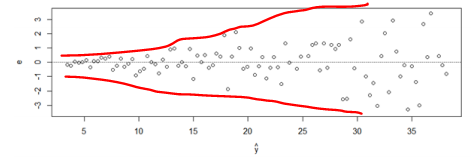
잔차그림을 보았을 때 퍼져있는 정도가 다른 것을 알 수 있습니다.
이 경우에 등분산성을 만족하지 않습니다.
대안으로 반응변수의 변환이 있습니다.
y값을 그대로 사용하지 않고 변환하는 것입니다.

이처럼 log로 변환하면 어느정도 등분산성을 만족하게 됩니다.
b. $\hat{y}$가 커지면서 e가 하강(상승)하다가 상승(하강)함

이 경우에 설명변수의 제곱항이 색략되어 있을 가능성이 큽니다.
또한 등분산성을 만족하지 않습니다.
대안으로 제곱항을 추가하거나 변수변환방법이 있습니다.
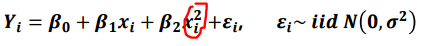
이처럼 제곱항을 추가하면 어느정도 등분산성을 만족하게 됩니다.
4. 등분산성 검정
등분산성 가정 하에서 $\sigam^2$를 MSE로 추정하게 됩니다.
등분산성을 잔차그림을 통해 시각적으로 확인할 수 있고, 문제를 파악할 수 있습니다.
수치적인 검정 방법은 Breusch-Pagan 검정이 있습니다.
5. 정규성 검정
시각적인 정규성 검정 방법은 히스토그램, Q-Q plot 등이 있습니다.
수치적인 정규성 검정 방법은 Shapiro-Wilk검정, Jarque-Bera 검정 등이 있습니다.
Q-Q plot에 대해 알아보겠습니다.
(1) 정규성을 만족하는 Q-Q Plot

데이터의 분포가 직선안에 모여있다는 것을 확인할 수 있습니다.
이 경우에 정규성을 만족한다고 볼 수 있습니다.
(2) 정규성을 만조갛지 않는 Q-Q Plot

이 경우에 데이터가 정규분포를 따른다고 보기 어렵습니다.
6. 독립성 검정
시각적으로 독립성을 파악하는 방법은 오차 앞뒤 간의 관계를 파악하기 위해 산점도를 그려보는 방법이 있습니다.
수치적으로 독립성을 파악하는 방법은 Durbin-Watson 검정, ACF 등이 있습니다.
자료가 시간순으로 관측된 경우(시계열자료) $e_{t-k}, e_t$의 산점도를 확인하겠습니다.
이는 앞뒤 간의 관계를 파악하여 독립성을 파악하는 방법입니다.
잔차 데이터 간에 상관관계가 없으면 독립하다고 가정할 수 있습니다.

오른쪽의 경우 독립성을 만족한다고 볼 수 있습니다.
7. 잔차검진 정리
분석에 사용된 회귀모형의 적절성과 통계적 추론의 가정을 만족하는지를 확인하는 방법에 대해 알아보았습니다.
