딥러닝 공부방

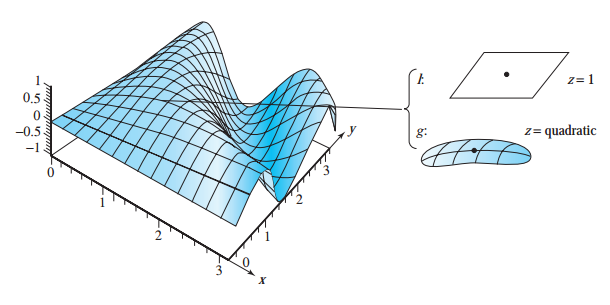
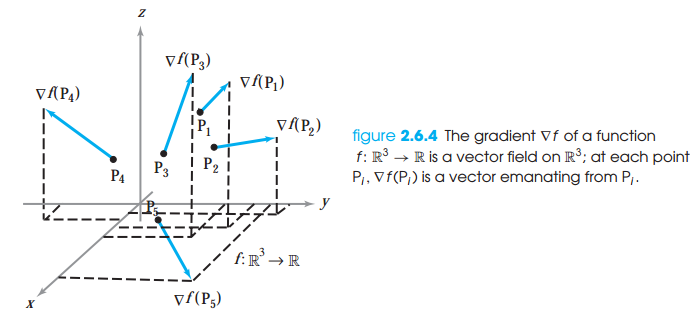
제약조건(constraint) 또는 추가조건(side condition)이 주어진 상황에서 함수의 최대값이나 최소값을 구해야하는 경우가 있습니다. 예를 들어 $x^2 + y^2 = 1$ 조건에서 함수 f(x,y)의 최대값을 찾는 경우입니다. 이 경우에 (x,y)는 g(x,y) = 1 의 등위선(level curve) 입니다. 이번 포스팅에서 이런 종류의 문제를 다루는 방법에 대해 공부하겠습니다. 라그랑주 승수법(Lagrange Multipliers) S는 x가 g(x) = c를 만족하는 R^n의 집합이라고 하겠습니다. f의 정의역을 S로 제한할 때도 f의 극소값, 극대값은 유효하여 최대, 최소값은 극값이 됩니다. 다음 정리는 제약조건에서 극값을 구하는 데 필요조건을 제공합니다. flS는 함수 f의 정의역..

이계도함수 판정법(Second-Derivative Test for Local Extrema) 임계점(x0)에서 함수의 이차 편미분 행렬인 헤시안이 양의 정부호(positive definite)이면 x0은 극소점(relative minimum) 입니다. 비슷하게, 임계점에서 함수의 헤시안이 음의 정부호이면 x0은 극대점(relative maximum)입니다. 헤시안 행렬이 양의 정부호, 음의 정부호를 판단하는 방법은 다음과 같습니다. a가 0보다 크고, B의 determinant가 0 이상이면 헤시안 행렬은 양의 정부호 입니다. 만약, a가 0보다 작고 determinant가 0보다 크면 해시안 행렬은 음의 정부호 입니다. 2x2 보다 큰 nxn 크기의 해시안 행렬에서 양의 정부호는 다음과 같이 판별할 수..

해시안(Hessian) 일변수함수에서 임계점 중 극점이 되는 판별법은 f''(x0) > 0 이면 극대점, f''(x0) < 0 이면 극소점 입니다. 하지만 다변수함수에서 이계편도함수(second derivative)는 상당히 복잡합니다. 이를 위해 헤시안(Hessian)이라고 불리는 이계편도함수의 표현법을 소개하겠습니다. 이 해시안은 이차 함수(Quadratic function)과 관련이 있습니다. 다음과 같이 표현되는 경우에 이차 함수(Quadratic function)라고 합니다. 이를 행렬의 곱으로 나타내면 다음과 같습니다. 만약 3개의 변수를 받는 경우, n =3은 다음과 같습니다. 이것을 이차 함수(quadratic function)이라고 합니다. [aij]는 대칭 행렬이라고 가정합니다. 이제 ..

극점의 일계도함수 판정법(First-Derivative Test for Local Extrema) 모든 극점(extremum)은 임계점(critical point) 입니다. 함수 f가 n개의 변수를 취하는 실함수이고 미분가능(differentiable)합니다. 그리고 점 x0에서 극점(local extremum)을 갖는다면 Df(x0)=0 이 됩니다. 즉, x0은 함수 f의 임계점(critical point)입니다. 만약 함수의 최대 최소값이나 극점을 찾으려 할때, 임계점들만 고려하면 됩니다. 함수의 최대값과 최소값을 찾는 몇 가지 예제를 풀어보겠습니다. 위 함수에서 임계점은 (0,0)만 존재합니다. 그리고 f(x,y) >= 0 이기 때문에 (0,0) 은 극소점(relative minumum)이 됩니다...

자연 현상에서 많은 것들은 최대최소작용의 결과입니다. 이번 포스팅에서는 함수의 최대 최소를 찾는 방법을 공부하겠습니다. 극값(Extreme Points) 함수의 그래프에서 가장 기본적인 기하학적 특징은 극값(extreme points) 입니다. 함수는 극값에서 최대, 최소값을 얻습니다. 이러한 극값을 찾는 방법을 알아보겠습니다. 위 정의를 살펴보면 x0의 근방 V에 존재하는 모든 x에 대하여 함수 f(x) >= f(x0)을 만족하는 점 x0을 극소점(local minimum)이라고 부릅니다. 반대로 f(x)

이전 포스팅에서는 일변수함수에 대한 테일러 정리를 살펴보았습니다. 이번에는 다변수함수에 대한 테일러 정리를 공부하겠습니다. 다변수함수에 대한 테일러 정리(Taylor's Theorem for Many Variables) 만약 n개의 변수를 취하는 실함수(real valued function with n variables) f가 x0에서 정의된다면 다음과 같이 정의할 수 있습니다. 그리고나서, 미분가능성의 정의에의해 나머지항 R1(x0,h)는 점 x0에서 1차에서 사라집니다. 그러므로 일차 테일러 공식(First-Order Taylor Formula)는 다음을 얻습니다. xi는 n개의 다변수에 해당하는 변수입니다. 각 개별적인 다변수에대해 hi가 존재합니다. 이차 테일러 공식은 다음과 같습니다. 이차 테일..

이전에 도함수를 공부할 때, 함수의 선형 근사(linear approximation)은 접평면의 방정식과 함수의 근사치를 찾는데 사용되었습니다. 여기서 공부할 테일러 정리(Taylor's theorem)은 이차근사(quadratic approximation)이나 고차근사(higher-order approximation)을 찾는 데 중요하게 다뤄집니다. 테일러 정리는 함수의 정확한 수치적 근삿값을 찾는데에 핵심적인 도구입니다. 이 테일러 정리를 다변수 함수의 최대, 최소에 대한 이계도함수 판정법(second derivative test)를 이해하는데 사용합니다. 다변수 함수에 대한 테일러 정리를 알아보기전에 일변수함수에 대한 테일러 정리를 살펴보겠습니다. 일변수함수에 대한 테일러 정리(Single-Vari..

반복 편도 함수(Iterated partial derivatives) 편미분이 존재하고, 이 편미분이 연속적인 경우에 이 함수를 class C1이라고 합니다. 만약 이 각각의 편도 함수가 다시 연속적인 편도 함수를 갖고 있다면 class C2라고 합니다. 계속 확장하여 함수는 class C3, class C4 라고 불릴 수 있습니다. 만약, 함수 f가 연속적인 3차 반복 편도 함수를 갖고 있다면 이는 class C3 입니다. 여기서 이계편도함수의 몇 가지 예제를 살펴보겠습니다. 삼계도함수나 고계도함수도 같은 방법으로 나타낼 수 있습니다. f가 두 변수 x와 y의 함수이고, 편미분이 연속적으로 미분가능하면 이 함수의 편도함수는 다음과 같은 네 개의 함수를 얻습니다. 이 네개를 반복 편도함수(iterated..

레벨 집합에서 그래디언트와 접평면(Gradients and Tangent Planes to Level Sets) level surface와 함수 f의 그래디언트 사이의 관계를 살펴보겠습니다. level surface는 함수 f의 값을 상수로 두고, 그 상수를 만족하는 점들의 집합을 나타낸 것입니다. 그래디언트는 함수 f의 값이 가장 빠르게 변화하는 방향을 나타냅니다. 이에반해 level surface는 f의 값이 전혀 변하지 않는 방향으로 놓여져 있습니다. level surface와 그래디언트는 직교합니다. 그래디언트와 level set은 수직이라는 것을 알았습니다. 그래디언트에 수직인 평면인 접평면을 정의하는 법을 알아보겠습니다. 그래디언트와 level surface는 수직이므로, 둘을 내적하면 0이 ..

3개의 변수를 받아 하나의 scalar를 출력하는 실함수(real-valued function with three variables) f가 존재한다고 가정하겠습니다. v와 x는 고정된 벡터라고 할때, 함수 f(x + tv)는 t값만 정해진다면 scalar를 출력할 수 있습니다. x + tv 형태의 모든 점의 집합은 점 x를 통과하고 벡터 v와 평행한 선 L 입니다. 방향 도함수(Directional Derivatives) 함수 t -> f(x + tv)는 선 L에 제한된 함수 f를 나타냅니다. 함수 f의 입력값이 선 L의 집합에 제한되어 있기 때문입니다. 만약, 새가 속도 v로 선(x + tv)을 따라 비행한다면, x + tv는 시간 t에서 새의 위치가 됩니다. 선 L을 따라 변화하는 함수 f의 값이 점..