
3개의 변수를 받아 하나의 scalar를 출력하는 실함수(real-valued function with three variables) f가 존재한다고 가정하겠습니다. v와 x는 고정된 벡터라고 할때, 함수 f(x + tv)는 t값만 정해진다면 scalar를 출력할 수 있습니다. x + tv 형태의 모든 점의 집합은 점 x를 통과하고 벡터 v와 평행한 선 L 입니다.
방향 도함수(Directional Derivatives)
함수 t -> f(x + tv)는 선 L에 제한된 함수 f를 나타냅니다. 함수 f의 입력값이 선 L의 집합에 제한되어 있기 때문입니다. 만약, 새가 속도 v로 선(x + tv)을 따라 비행한다면, x + tv는 시간 t에서 새의 위치가 됩니다.
선 L을 따라 변화하는 함수 f의 값이 점 x에서 얼마나 빠르게 변화하는지 궁금할 수 있습니다. 함수의 변화률은 미분으로 주어지기 때문에, 이 질문은 t=0에서 함수를 t로 미분한 값이라고 대답할 수 있습니다. 즉, 선 L의 방향으로 점 x에서 함수 f의 미분은 다음과 같이 공식화 할 수 있습니다.

x에서 방향 v으로 함수 f의 방향 도함수는 다음과 같이 계산합니다.
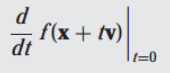
방향 도함수의 정의에서 벡터 v는 일반적으로 unit vector로 선택합니다. 이 경우에 v 방향으로 unit 속도로 이동한다고 생각할 수 있습니다.
방향 도함수는 또한 다음과 같이 정의될 수 있습니다.

만약, 함수 f가 미분 가능하면 모든 방향 도함수는 존재합니다. 방향 v으로 x에서 방향 도함수는 다음과 같이 계산합니다.

여기서, v = (v1, v2, v3) 입니다.
위 공식은 다음과 같이 증명합니다. c(t) = x + tv 라고 하겠습니다. 그러면 f(x + tv) = f(c(t))가 됩니다. f(c(t))를 연쇄 법칙으로 t=0에서 미분하면 다음과 같이 됩니다.

경로 c(t) = x + tv에 대하여 c(0) = x, c'(0) = v가 됩니다.
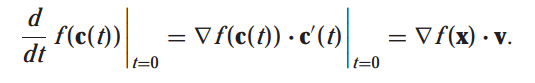
예제 문제를 풀어보겠습니다.

가장 빠른 증가 방향(Directions of Fastest Increase)

함수 f의 gradient는 함수 f가 가장 빠르게 증가하는 방향을 가르킵니다. 즉, f가 가장 빠르게 증가하는 방향으로 움직이고 싶으면 $\triangledown$f(x) 방향으로 나아가면 됩니다. 유사하게 f가 가장 빠르게 감소하는 방향으로 이동하고 싶으면, -$\triangledown$f(x) 방향으로 나아가면 됩니다.
예시 문제를 풀어보겠습니다.

참고자료 및 그림 출처
Jerrold E. Marsden의 Vector Calculus