선형근사(Linear Approximation)
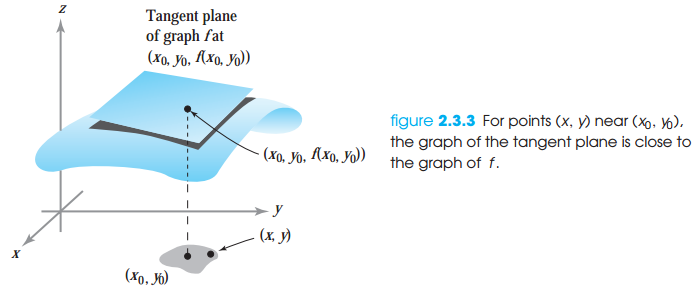
다변수 함수 f가 충분히 매끄러울 때, 점(x_0, y_0)에서 함수의 그래프에 접하는 평면의 방정식을 구해보겠습니다. 수직이 아닌 평면의 방정식은 다음의 형태를 갖습니다.

만약 위 식이 함수의 그래프에 접하는 평면이라면 x와 y축을 따르는 기울기는 x와 y에 대한 함수 f의 변화율인 af/ay와 af/ax와 같아야 합니다. 따라서 a와 b는 다음과 같아야 합니다.

상수 c는 x=x0, y=y0인 경우에 z = f(x0, y0)이라는 사실로부터 구할 수 있습니다. 따라서 선형 근사(linear approximation)은 다음과 같이 구할 수 있습니다.

위 방정식은 만약 f가 충분히 smooth한 경우에 (x0, y0)에서 함수 f의 그래프에 접하는 평면의 방정식입니다. 미분 가능성에 대한 정의는 선형근사에 의해 정의된 평면이 (x0, y0) 가까이에서 함수 f의 좋은 근사임을 의미합니다.
좋은 근사가 무엇인지 이해하기 위해서 일변수 미분(one-variable calculus)를 잠시 살펴보겠습니다. 만약 함수 f가 x0에서 미분가능하면 다음과 같습니다. (x0)에서 함수의 그래프와 접하는 접선을 구하는 식입니다.
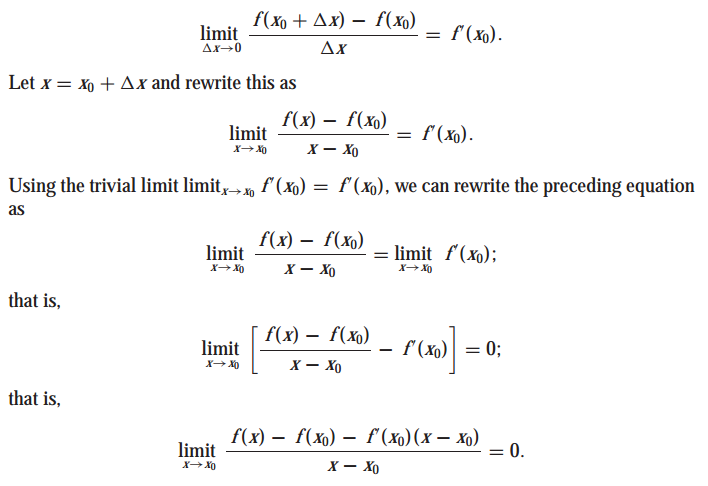

x0에서 f(x0)과 l(x0)은 비슷한 값을 갖습니다. 이것이 일변수 함수에서 좋은 근사를 의미했습니다. 다변수 함수에서는 접선을 대신하여 접평면으로 좋은 근사의 개념을 적용합니다.
이변수 함수에 대한 미분가능성(Differentiabillty for Functions of Two Variables)
위에서 살펴본 선형근사를 사용하여 이변수함수에 대한 미분가능성 개념을 정의합니다.

점 x0, y0에서 함수 f(x0,y0)과 선형근사 값의 차이가 0에 가까우면 함수 f는 미분가능하다고 합니다. 이변수함수에서 함수 f의 선형근사는 접평면으로 정의됩니다. x0, y0에서의 접평면과 f(x0,y0)의 값이 비슷하다면 함수 f는 x0,y0에서 미분이 가능합니다. 그리고 이 경우에 접평면 방정식은 함수 f의 좋은 근사임을 말합니다.
접평면(Tangent Plane)
미분가능성을 정의하기 위해 함수의 그래프에 접하는 평면에 대한 공식적이지 않은 개념을 사용했습니다. 여기서 접평면의 엄밀한 정의를 살펴보겠습니다.

접편면을 구하는 예시문제를 풀어보겠습니다.

접평면에서 a와 b는 함수 f의 x에 대한 편미분과 함수 f의 y에 대한 편미분입니다. 이것을 Df(x0,y0) 행렬로 나타내면 다음과 같습니다.

Df(x0,y0)을 사용하면 미분가능성의 정의에 대한 방정식은 다음과 같이 주어집니다.

이처럼 이변수함수에서 미분가능성의 정의를 행렬로 표현할 수 있습니다. 그리고 이 것은 (x0, y0)에서 함수 f의 좋은 근사입니다. 좋은이라는 표현은 근사식과 f(x,y)의 차이가 아래 식의 상수배인 경우를 의미합니다.
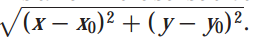
참고자료 및 그림 출처
Jerrold E. Marsden의 Vector Calculus
'수학 > 벡터 미적분학' 카테고리의 다른 글
| [벡터 미적분학] 연쇄 법칙(Chain rule) (0) | 2021.06.16 |
|---|---|
| [벡터 미적분학] 미분 가능성(Differentiable), 그래디언트(Gradient), C1 함수(C1-Function) (0) | 2021.06.04 |
| [벡터 미적분학] 편도 함수(Partial Derivatives) (0) | 2021.06.03 |
| [벡터 미적분학] 극한(Limits)과 극한의 성질(Properties of Limits) (0) | 2021.06.02 |
| [벡터 미적분학] 경계점(Boundary Points) (0) | 2021.06.01 |