일반적인 경우에서 미분가능성(Differentiable: The General Case)
이전 포스팅에서는 이변수함수에 대한 미분가능성(Differentiability for Functions of Two Variables)에 대해 살펴보았습니다. 이번에는 R^n에서 R^m으로의 함수 f에 대한 미분 가능성을 정의하겠습니다.
접평면을 구하는 방법에서 Df(x,y)를 공부했었습니다.
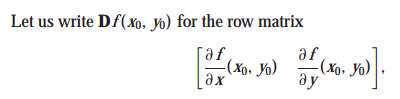
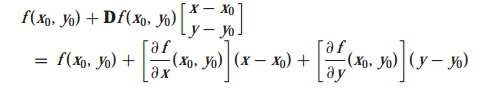
점 x0에서 함수 f = (f1, ... , fm)의 도함수 Df(x0)은 성분이 x0에서 t_ij = af_i/ax_j인 행렬 T 입니다.

R^n에서 R^m으로의 함수 f가 두 가지 조건을 만족하면 미분 가능하다고 정의합니다.
(1) x0에서 편미분이 존재해야 합니다.
(2) 아래의 극한이 만족해야 합니다.
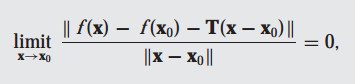
여기서 T는 Df(x0)을 의미하며, Df(x0)은 x0에서 함수 f의 편미분 행렬이라고 부릅니다.
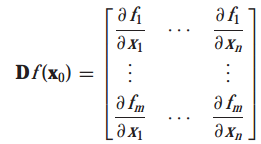
함수 f(x)에서 선형 근사식을 뺀 후에 x-x0 거리를 나눴을 때, x - > x0 극한이 0을 만족하는 것을 의미합니다. 만약에 x0에서 함수 f가 미분가능하다면 선형 근사식은 접평면이 됩니다. 접평면을 정의한 후에 미분가능성을 정의하는 것이 아니라 미분 가능성을 정의한 후에 접평면을 정의합니다.
예제를 한번 풀어보겠습니다. 주어진 함수의 편미분 행렬을 구하는 문제입니다.
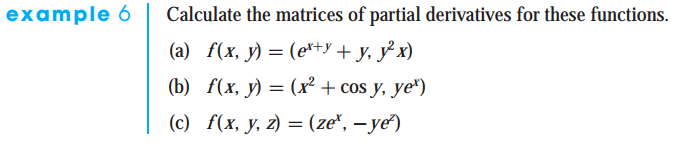
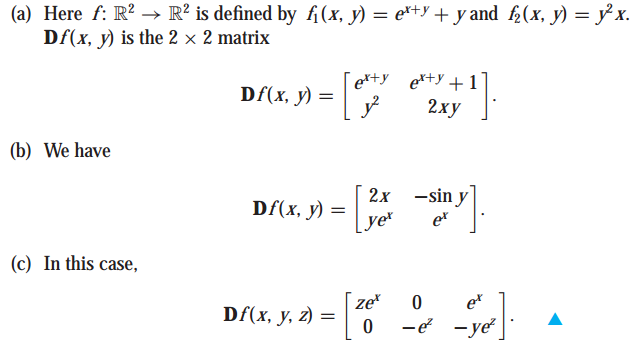
그래디언트(Gradient)
실함수의 도함수의 경우에 특별한 용어를 사용합니다. 실함수는 R^n에서 R^1으로의 함수를 의미합니다.

즉, 함수 f가 실함수인 경우에 f의 편미분 행렬을 그래디언트라고 부르고 다음과 같이 표기합니다.

h가 x-x0을 의미하는 경우에 f(x0) + Df(x)(h)는 선형근사식을 의미합니다. Df(x)를 그래디언트로 다음과 같이 표현할 수 있습니다.
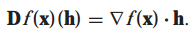
그래디언트를 계산하는 예제 문제를 살펴보겠습니다.
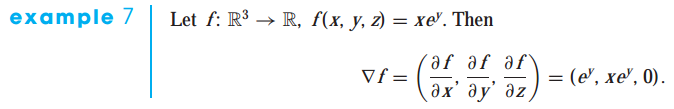
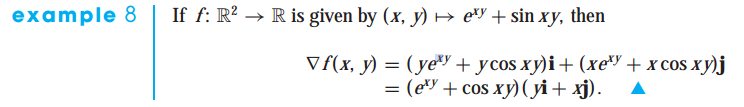
한 점에서 편미분이 존재한다고 해당 점에서 연속적인 것은 아닙니다. 또한 함수가 연속적이라고 미분 가능한 것은 아닙니다.
일변수 함수 f(x) = lxl 인 경우에 함수가 연속적이지만 미분 가능하지 않습니다.
이변수 함수에서 편도함수는 존재하지만 그 점에서 연속이 아닌 이변수 함수 예제입니다.

함수 f가 0,0에서 편도함수가 존재합니다. 하지만 0,0에서 연속적이지 않습니다. 즉, 편도 함수가 존재한다고 해서 해당 점이 연속적인 것은 아닙니다.
몇 가지 기본 정리들(Some Basic Theorems)
미분가능성(differentiability)와 연속성(continuity)와 관련된 몇 가지 기본 정리를 살펴보겠습니다.
(1)

만약 함수 f가 x0에서 미분가능하면, 함수 f는 x0에서 연속적입니다. 미분가능성은 접평면을 가질 정도로 부드럽다는 것을 의미하며 이는 연속적인 것보다 더 강한 의미를 갖습니다.
(2)
위에서 살펴보았던 미분가능성에 대한 정의는 증명하기 어려울 떄가 있습니다. 선형 근사식을 세워야하고 극한을 증명해야 하기 때문입니다. 따라서 함수가 미분가능하다는 것을 간단히 말해주는 이론을 살펴보겠습니다. 주의할 점은 이 이론이 미분가능성의 정의를 대체하는 것이 아닙니다. 아래 조건을 만족하는 경우에 미분이 가능하다고 말할 수 있습니다.

x의 근방 모두에서 함수 f의 편도함수가 존재하고 이 편도함수가 연속적이라면, 함수 f는 x에서 미분 가능합니다. 그리고 이 조건에 해당하는 함수를 C1 function이라고 부릅니다. 즉, 함수가 C1 함수인 경우에 미분이 가능합니다. 포스팅 앞에서 설명한 복잡한 미분가능성 정의를 증명하지 않고, c1 함수인지 판별을 하면 미분가능한지 판단할 수 있습니다. c1 함수가 아니라고 미분이 불가능한 것은 아닙니다.
함수의 미분가능성을 증명하는 경우에 아래와 같은 절차로 진행할 수 있습니다.
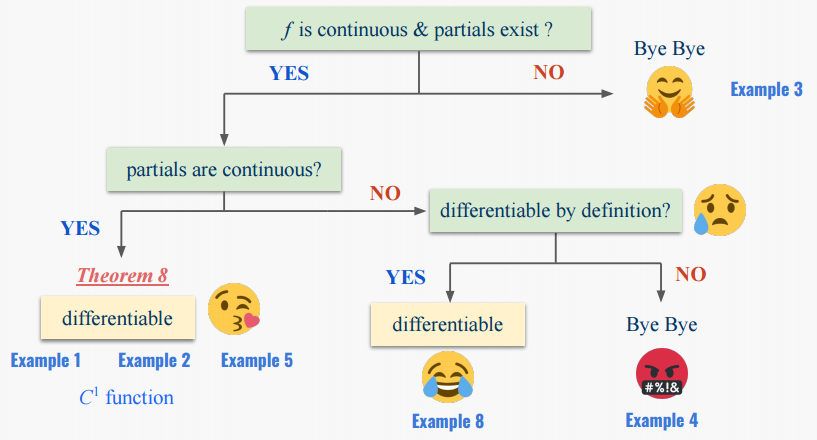
우선 함수 f가 연속적이고, 편미분이 존재해야 합니다. 이 조건에 해당하는 경우에 편미분이 연속적인지 확인합니다. 연속적이면 c1 함수이므로 미분가능합니다. 편도함수가 연속적이지 않은 경우에 극한과 선형근사식을 활용하는 미분가능성의 정의를 사용하여 미분가능성을 판단합니다.
참고자료 및 그림 출처
Jerrold E. Marsden의 Vector Calculus
인프런 벡터 미적분학 강의
'수학 > 벡터 미적분학' 카테고리의 다른 글
| [벡터 미적분학] 방향 도함수(Directional Derivatives) (0) | 2021.06.29 |
|---|---|
| [벡터 미적분학] 연쇄 법칙(Chain rule) (0) | 2021.06.16 |
| [백터 미적분학] 선형근사(Linear approximation), 접평면(Tangent Plane), 이변수함수의 미분가능성 (0) | 2021.06.03 |
| [벡터 미적분학] 편도 함수(Partial Derivatives) (0) | 2021.06.03 |
| [벡터 미적분학] 극한(Limits)과 극한의 성질(Properties of Limits) (0) | 2021.06.02 |