(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다.
(k-mooc 통계학의 이해1, 여인권)을 수강하면서 정리해보았습니다.
자료들 간의 거리를 이용하여 산포도를 계산하는 방법(표본분산, 표본표준편차)을 알아보겠습니다.
자료분석에서 측정 단위에 영향을 받지 않게 만드는 표준화에 대해 알아보겠습니다.
그리고 평균으로 표본표준편차를 보정한 변동계수를 알아보겠습니다.
(3) 표본분산과 표본표준편차
범위나 사분위수범위의 경우 특정 위치의 두 값을 이용하기 때문에 표본의 정보를 많이 활용하지 못합니다. 이런 문제를 해결하기 위해 모든 자료들 간의 거리의 합을 이용하는 것 입니다.
수학적으로 거리 $D$는 임의의 점 a, b, c에 대해 다음과 같은 성질을 만족합니다.

우리는 거리$D$의 성질 중 $D$(a, b) = $\mid{a-b}\mid$와 $D$(a, b) = ${(a-b)}^2$에 관심을 갖겠습니다. 이를 이용하면 모든 관측값들 간 거리의 합을 다음과 같이 계산할 수 있습니다.

자료들이 넓게 퍼져 있으면 이 합들은 큰 값을 가질 것이고 모여 있으면 작아질 것입니다.
위의 식을 사용하기 위해서는 $n^2$개의 거리 합을 계산해야 하므로 $n$이 커지면 계산의 부담이 생길 수 있어 아래와 같이 임의의 중심위치 $a$에서 자료를이 떨어져 있는 거리의 합을 생각해 볼 수 있습니다.

이렇게 하면 자료들의 모든 정보를 사용하면서 자료들이 $a$를 중심으로 얼마나 펴져 있는지를 나타낼 수 있습니다. 즉, 자료들이 $a$를 중심으로 모여 있으면 위의 합은 작아지고 반대로 넓게 퍼져 있으면 커지게 됩니다.
위의 식을 사용하기 위해서는 $a$값을 정해야 하는데 이 중심위치 선택은 매우 중요합니다.
먼저 $L_2$에서 $a$를 선택하는 방법을 알아보겠습니다. $L_2$($a$)에서 $a$가 좋은 중심위치가 되려면 자료들과의 거리가 가능한 짧아야 하며 결국 모든 자료들과의 거리 합을 최소로 만드는 값이 되어야 합니다. 이런 조건을 만족하는 $a$는 다음과 같이 $L_2$($a$)를 $a$에 대해 미분한 식이 0이 되는 값입니다.

결론적으로 $a$ = $\overline{x}$가 되는데 이는 $L_2$($a$)에서는 중심위치로 표본평균 $\overline{x}$가 적절하다는 것을 의미합니다.
$L_1$($a$)의 경우 $a$로 미분할 수 없기 때문에 다른 방법을 이용해야 합니다.

왼쪽 그림을 보면 자료가 2개 있을 때 $L_1$($a$) = $L_1$($b$) + 2$k$가 되어 $L_1$($b$)가 $L$($a$)보다 작은 것을 알 수 있습니다. 이를 일반화하면 표본크기가 짝수이면 $a$가 중간에 있는 두 값의 사이에 있어야 $L_1$($a$)가 최소가 됩니다.
자료가 3개인 경우에는 $L_1$($a$) = $L_1$($b$) + $k$가 되며 $L$($b$)가 $L$($a$)보다 작은 것을 볼 수 있습니다. 이를 일반화하면 표본크기가 홀수일 때 $a$는 표본의 중앙에 있어야 한다는 것을 알 수 있습니다.
결론적으로 $L_1$($a$)를 최소로 만드는 $a$는 표본중앙값 $\widetilde{x}$가 됩니다.
정리를 해보면 $L_1$일 때에는 표본중앙값 $\widetilde{x}$, $L_2$인 경우에는 표본평균 $\overline{x}$가 중심위치로 사용됩니다. 이를 정리하면 퍼져 있는 정도를 나타내는 통계값으로

가 이용됩니다.
$L_2$는 편차의 제곱합으로 표시됩니다. $L_2$는 자료가 추가되면 계속 커지므로 표본크기로 보정을 해주어야 합니다.
표본분산(sample variance)은 $L_2$에서 보정을 위해 n-1로 나눈 값 입니다.

여기서 표본크기 n이 아닌 n-1로 나눈 이유는 편차의 합은 0이기 때문에 n-1개의 편차만 자유롭게 값을 가질 수 있고 마지막 편차는 합이 0이 되게 만드는 역할을 하기 때문입니다. 이 n-1을 자유롭게 가질 수 있는 편차의 개수라고 해서 자유도(deferr of freedom)이라고 합니다.
표본분산을 계산할 때 편차의 제곱식을 다음과 같이 전개시키면 계산이 좀더 간단해집니다.
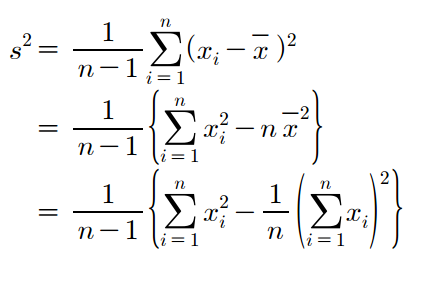
표본분산은 편차의 제곱합을 이용하기 때문에 분산의 단위는 관측값 단위의 제곱이 되어 표본분산의 값을 보고 자료가 얼마나 퍼져 있는지 직관적으로 파악하기 어렵습니다. 우리가 눈으로 이해하는 산포와 일치시키려면 자료를 측정할 때의 단위로 변환시켜 표시해야 합니다. 이를 표본분산을 제곱근을 취해 구할 수 있습니다. 이를 표본표준편차(sample standard deviation)라고 합니다.

이번에는 표준화에 대해서 알아보겠습니다.
수능시험은 과목별로 난이도가 다를 수 있기 때문에 원점수로 과목 간 성적을 비교하면 문제가 있을 수 있습니다. 이런 경우 아래와 같이 원점수에 평균을 빼고 표준편차를 나누어 점수를 표준화하여 절대비교를 합니다.

표준화 과정을 거치면 표준화점수의 표본평균은 0 이되고 표본분산은 1이 됩니다.

즉, 표준화는 평균이 0, 표준편차가 1이 되도록 만듭니다. 이를 통해 측정 단위에 영향을 받지 않게 중심위치와 척도(scale)를 조정하고 절대비교를 할 수 있게합니다.
(4) 변동계수(CV, coefficient of variation)
변동계수(CV)는 평균으로 표본표준편차를 보정한 것을 의미합니다. 변동계수(CV)는 다음과 같이 나타낼 수 있습니다.

자료를 분석하다 보면 표준편차가 평균에 영향을 받는 경우가 있습니다. 예를 들어, 후진국의 소득분포와 선진국의 소득분포를 비교한다고 해보겠습니다. 일반적으로 선진국 소득의 표준편차가 후진국의 표준편차보다 훨씬 큰데 그 이유는 비교 그룹 간의 평균이 큰 차이가 있고 평균이 커지면 산포 또한 커지는 경향을 가지는 자료이기 때문입니다.
이런 경우 표준편차 자체만 이용하여 산포를 비교하는 것은 적절하지 않을 수 있기 때문에 다음과 같이 평균으로 표본표준편차를 보정한 변동계수(corfficient of variation)를 사용할 수 있습니다. 변동계수에 100을 곱하여 표본평균에 비해 표본표쥰편차가 얼마나 큰지를 % 개념으로 표시하는 경우도 있습니다. 변동계수는 신장과 체중과 같이 단위가 전혀 다른 자료들의 퍼져 있는 정도를 비교할 때에도 사용합니다.
이상으로 수치자료 분포의 산포를 나타내는 표본분산, 표본표준편차, 표준화, 변동계수를 알아보았습니다. 감사합니다.
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 03-1. 다변량 자료 기술통계 (1) - 분할표, k차원 분할표, 원도표, 막대그래프 (0) | 2020.09.14 |
|---|---|
| [통계학] 02-8. 기술통계 (8) - 수치자료의 형태 (왜도, 첨도, 꼬리) (0) | 2020.09.14 |
| [통계학] 02-6. 기술통계 (6) - 수치자표 분포의 산포1 (범위, 사분위범위, 상자그림) (0) | 2020.09.13 |
| [통계학] 02-5. 기술통계 (5) - 수치자료의 대체중심위치(중앙값, 절사평균, 최빈값) (0) | 2020.09.13 |
| [통계학] 02-4. 기술통계 (4) - 수치자료 분포의 중심위치(평균, 표본비율, 기하평균, 조화평균, 가중평균) (0) | 2020.09.13 |