이번에 고유치가 복소수일 때 어떤 성질을 지니게 되는지 공부해보겠습니다.
1. 복소수 공간에서 행렬의 고유치-고유벡터 이론 - Matrix Eigenvalue-Eigenvector Theory for $C^n$
이전까지 $R^n$ 공간에 있는 eigenvalues와 eigenvector에 대해 공부해보았습니다.
그러면 eigenvalues와 eigenvector가 $C^n$ 공간에 있는 경우에 어떻게 작용되는지 알아보겠습니다.
$R^n$ space에 있는 이론이 그대로 적용되어 정의도 같습니다.
단지, eigenvalue가 complex value를 갖게 될 뿐입니다.
복소수 scalar $\lambda$가 det(A-$\lambda$I) = 0을 만족하면 Ax = $\lambda$x 에서 $C^n$ space에 존재하는 nonzero vector x 가 존재합니다.
이 complex eigenvalue는 시각적으로 신기하게 나타납니다.
예시 문제 1
A가 다음과 같이 주어졌을 때 A의 eigenvalue는 다음과 같습니다.

characteristic equation으로 $\lambda$를 구할 수 있습니다.

$\lambde$ = i, -i가 되고 이는 conjugate(켤레 복소수) 관계에 있습니다.
eigenvalue에 해당되는 eigenvector를 구하면 다음과 같습니다.
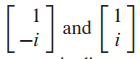
eigenvector도 conjugate 관계에 있습니다.
이처럼 eigenvalue와 eigenvector에서 complex부분이 conjugate 관계에 있다는 특징을 확인할 수 있습니다.
예시 문제 2
이번에는 complex eigenvalue가 존재하는 행렬 A로 linear transformation을 했을 때, 시각적으로 어떻게 변화되는지 확인해보겠습니다.

A가 위와 같이 주어졌을 때 eigenvalue를 찾고 eigenspace에서의 basis를 찾아보겠습니다.
우선, A의 characteristic equation으로 eigenvalue를 찾습니다.


A-$\lambda$I로 eigenvalue에 해당하는 eigenvector를 찾겠습니다.

row reduction을 통해 general solution을 구합니다.


x2 = 5일때 x1 = -2 -4i가 됩니다.
이것이 $\lambda$ = 0.8 - 0.6i 일때의 eigenvector 입니다.

$\lambda$ = 0.8 + 0.6i 일때의 eigenvector는 conjugate 관계에 있으므로 다음과 같습니다.

이제 x = (2,0) 일때 Ax를 반복수행 해보겠습니다.

이것을 시각적으로 표현하면 다음과 같이 됩니다.
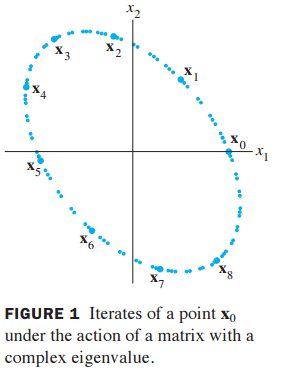
타원 형태가 나타나게 됩니다.
이것이 complex eigenvalue의 특성입니다.
2. 복소수 공간에서 작동하는 실수 행렬의 고유치와 고유벡터 - Eigenvalues and Eigenvectors of Real Matrix That Acts on $C^n$
entires가 real인 nxn 행렬 A가 있을 때 $\lambda$가 complex space에 존재하면 다음이 성립합니다.

$\overline{A}, \overline{x}, \overline{\lambda}$는 conjugate를 의미합니다.
행렬 A에 complex eigenvalue가 주어지면 complex의 conjugate도 eigenvalue가 되고 그에 해당하는 conjugate vector도 eigenvector가 됩니다.
A가 real일 때, A의 complex eigenvalues는 conjugate pair입니다.
예시 문제 1
C가 다음과 같이 주어졌을 때 이것의 eigenvalue와 C로 인한 transformation이 어떻게 작동되는지 확인해보겠습니다.

C의 eigenvalues는 다음과 같습니다.

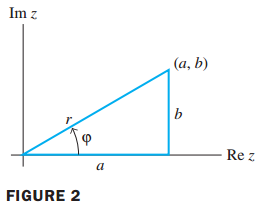
C를 다음과 같이 표현할 수 있습니다.

r = $\sqrt{a^2+b^2}$ 이며, 이는 transformation을 했을 때 scaling 값이 됩니다.
이제 complex eigenvalue를 갖는 행렬 C로 x를 transformation 해보겠습니다.

이처럼 rotation이 되고 scaling이 되었습니다.
a와 b에 따라서 scaling 크기가 다릅니다.
예시문제 2
complex eigenvalue를 갖고 있는 행렬 A는 eigenvalue의 real part와 imaginary part로 구성된 행렬 C와 similar 관계에 있습니다.
행렬 A가 다음과 같이 주어졌을 때 eigenvalue와 eigenvector를 구해보겠습니다.



A와 similar 관계에 있는 matrix를 찾기 위해 P를 다음과 같이 구할 수 있습니다.

이제 C = $P^{-1}AP$를 해보면 A와 similar 관계에 있는 행렬 C를 구할 수 있습니다.

C의 entries는 eigenvalue의 real part와 imaginary part가 됩니다.
또한 C 행렬으로 transformation을 적용하면 r = 1이므로 순수한 회전 동작만 작동합니다.

3. 이론 8. - Theorem8.

P는 eigenvector의 real part, imaginary part가 되고, C는 eigenvalue의 real part, imaginary part가 됩니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
