안녕하세요! 이번에 읽어볼 논문은 Soft-NMS, Improving Object Detection With One Line of Code 입니다.
NMS 문제점
[Object Detection] 비-최대 억제(NMS, Non-maximum Suppression)를 이해하고 파이토치로 구현하기
안녕하세요! 이번 포스팅에서는 비-최대 억제(NMS,Non-maximum Suppression)을 알아보도록 하겠습니다. 비최대 억제를 이해하기 위해서는 IoU(intersection over unio)에 대한 개념을 알아야합니다. IoU에..
deep-learning-study.tistory.com
Soft-NMS는 NMS의 문제점을 개선하기 위해 제안되었습니다. NMS에는 어떤 문제점이 존재할까요??
동일한 클래스를 지닌 여러 물체가 뭉쳐있는 경우에, 하나의 바운딩 박스만을 검출하고, 나머지 바운딩 박스는 억제합니다. NMS 알고리즘을 살펴보면, 해당 클래스에서 confidence가 가장 높은 바운딩 박스를 선택하고, 선택된 바운딩 박스와 IoU가 일정 이상인 박스들은 다 억제합니다. 따라서 동일한 클래스 여러 물체가 겹쳐있으면 하나의 바운딩 박스만 선택되고 나머지 바운딩 박스는 억제되는 것입니다.

왼쪽 그림을 보면 얼룩말이 두 마리 존재하지만, NMS 알고리즘에 의해서 하나의 얼룩말만 검출되었습니다. 반면에 Soft-NMS는 얼룩말 두마리를 잘 검출합니다.
Soft-NMS
Soft-NMS는 바운딩 박스를 억제하는 것이 아니라, confidence를 감소시킵니다. 기존의 NMS에서 억제되었던 바운딩 박스가 Soft-NMS를 적용하면 낮은 confidence로 검출되는 것입니다.

위 그림을 보면, 초록색 바운딩 박스는 NMS에 의해 억제되어야 하지만, Soft-NMS는 낮은 confidence를 부여합니다. 기존의 confidence가 0.8인데, 0.4로 감소하여 표현하는 것입니다.
Soft-NMS는 기존 NMS 알고리즘 코드에서 몇 가지만 변경하면 됩니다.

f(iou(M,bi)) 함수는 다양하게 적용할 수 있습니다. 논문에서는 두 가지 함수를 제시합니다.
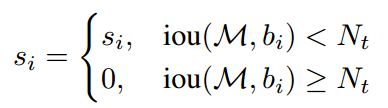
위 함수는 기존 NMS 함수입니다. M은 해당 클래스에서 confidence가 가장 높은 바운딩박스를 의미하며, bi는 동일한 클래스내의 박스를 의미합니다. M과 bi의 iou가 일정 값(Nt) 이상이면 0으로 억제됩니다.

논문에서 제안하는 첫 번째 Soft-NMS 함수입니다. M과 bi의 iou가 일정 값 이상일 때, 0으로 억제하는 것이 아닌 score를 감소합니다. 또한 M과 bi의 iou가 높으면 높은 가중치를 부여하고, iou가 낮으면 낮은 가중치를 부여합니다. 이 함수는 Nt 임계값을 기준으로 score가 급격하게 변하여 연속형 함수가 아니라는 단점이 존재합니다.

두 번째 함수입니다. 이 함수는 score가 연속형이라는 장점이 있습니다. 가우시안 분포를 활용합니다. 따라서 하이퍼 파라미터(sigma)가 하나 추가됩니다. 실험결과를 보면 이 gaussian soft-NMS가 더 좋은 성능을 나타냅니다.
PyTorch Code
Soft-NMS PyTorch 코드입니다. 출처: github.com/DocF/Soft-NMS/blob/master/softnms_pytorch.py
def soft_nms_pytorch(dets, box_scores, sigma=0.5, thresh=0.001, cuda=0):
"""
Build a pytorch implement of Soft NMS algorithm.
# Augments
dets: boxes coordinate tensor (format:[y1, x1, y2, x2])
box_scores: box score tensors
sigma: variance of Gaussian function
thresh: score thresh
cuda: CUDA flag
# Return
the index of the selected boxes
"""
# Indexes concatenate boxes with the last column
N = dets.shape[0]
if cuda:
indexes = torch.arange(0, N, dtype=torch.float).cuda().view(N, 1)
else:
indexes = torch.arange(0, N, dtype=torch.float).view(N, 1)
dets = torch.cat((dets, indexes), dim=1)
# The order of boxes coordinate is [y1,x1,y2,x2]
y1 = dets[:, 0]
x1 = dets[:, 1]
y2 = dets[:, 2]
x2 = dets[:, 3]
scores = box_scores
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
for i in range(N):
# intermediate parameters for later parameters exchange
tscore = scores[i].clone()
pos = i + 1
if i != N - 1:
maxscore, maxpos = torch.max(scores[pos:], dim=0)
if tscore < maxscore:
dets[i], dets[maxpos.item() + i + 1] = dets[maxpos.item() + i + 1].clone(), dets[i].clone()
scores[i], scores[maxpos.item() + i + 1] = scores[maxpos.item() + i + 1].clone(), scores[i].clone()
areas[i], areas[maxpos + i + 1] = areas[maxpos + i + 1].clone(), areas[i].clone()
# IoU calculate
yy1 = np.maximum(dets[i, 0].to("cpu").numpy(), dets[pos:, 0].to("cpu").numpy())
xx1 = np.maximum(dets[i, 1].to("cpu").numpy(), dets[pos:, 1].to("cpu").numpy())
yy2 = np.minimum(dets[i, 2].to("cpu").numpy(), dets[pos:, 2].to("cpu").numpy())
xx2 = np.minimum(dets[i, 3].to("cpu").numpy(), dets[pos:, 3].to("cpu").numpy())
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = torch.tensor(w * h).cuda() if cuda else torch.tensor(w * h)
ovr = torch.div(inter, (areas[i] + areas[pos:] - inter))
# Gaussian decay
weight = torch.exp(-(ovr * ovr) / sigma)
scores[pos:] = weight * scores[pos:]
# select the boxes and keep the corresponding indexes
keep = dets[:, 4][scores > thresh].int()
return keep
Performance
기존 NMS 보다 1~2% 정도의 성능 향상을 보입니다.




출처