안녕하세요! 오늘 읽은 논문은 Gaussian YOLOv3, An Accurate and Fast Object Detection Using Localization Uncertainty for Autonomous Driving 입니다.
YOLOv3을 기반으로 한 Gaussian YOLOv3은 바운딩 박스 좌표의 불확실성을 측정하여 불확실성, object score, class을 기준으로 최종 바운딩 박스를 선택합니다. 기존의 YOLOv3은 object score와 class만을 최종 바운딩 박스를 선택했기 때문에, 불확실성이 추가된 Gaussian YOLOv3이 더 좋은 정확도를 나타냅니다. 실제로 YOLOv3보다 FP(False Positive)를 낮추고 TP(True Positive)를 높이는 결과를 달성합니다.

Gaussian YOLOv3은 바운딩 박스의 불확실성을 측정하기 위해 Gaussian parameter을 추가하고, loss function을 수정합니다.
Gaussian modeling
기존의 YOLOv3은 바운딩 박스 좌표를 예측했다면, Gaussian YOLOv3은 좌표를 가우시안 분포로 고려하여 평균과 분산을 계산합니다. 즉, 좌표를 예측하는 것이 아니라 가우시안 분포의 모수를 예측하는 것입니다.
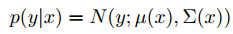
평균과 분산은 아래와 같이 계산하며 분산은 바운딩 박스의 불확실성을 나타냅니다.
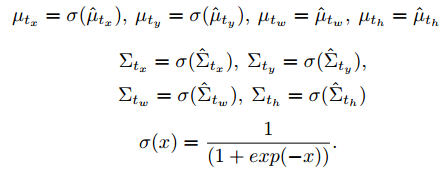
수식을 보면 일반적으로 생각하는 평균과 분산식과 다르다는 것을 확인할 수 있습니다. 실제 평균과 분산을 계산하는 것이 아니라 위의 수식으로 평균과 분산을 정의한 뒤에 loss function을 수정하여, 위 값이 평균과 분산의 의미를 갖게 하는 것입니다.
기존 YOLOv3이 예측한 x,y,w,h 좌표를 출력했다면 Gaussian YOLOv3은 시그모이드 함수를 적용하여 평균과 분산값의 의미를 갖도록 합니다. tw와 th의 평균은 시그모이드가 적용되지 않은 것을 확인할 수 있는데, tw와 th는 마이너스 값을 가질 수 있으므로 시그모이드를 적용하지 않습니다.
Reconstruction of loss function
Gaussian YOLOv3은 좌표값이 가우시안 분포를 갖는다고 가정하여 사후 확률을 계산하기 때문에, 음의 로그 가능도 손실함수를 사용합니다. object loss와 class loss는 기존의 YOLOv3과 동일합니다.
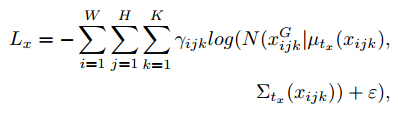
시그모이드로 계산한 평균과 분산이 손실 함수에서 정규분포의 모수로 사용하므로 실제 평균 분산 계산식이 아니여도 평균과 분산의 의미를 갖습니다. xG는 ground-truth를 의미합니다.
log 앞에 가중치 델타가 붙어있는 것을 확인할 수 있습니다. 이 가중치는 객체 크기에 따라 다른 값을 제공합니다.
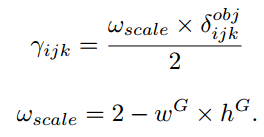
Utilization of localization uncertainty
예측한 불확실성을 어떻게 활용할까요?
최종 바운딩 박스의 socre을 다음과 같이 계산합니다. 기존의 YOLOv3에서 불확실성이 추가되었습니다.

불확실성이 추가된 score를 기준으로 nms를 적용하므로 좀 더 정확한 바운딩 박스를 가진 예측값을 최종 바운딩 박스로 선택하게 됩니다.
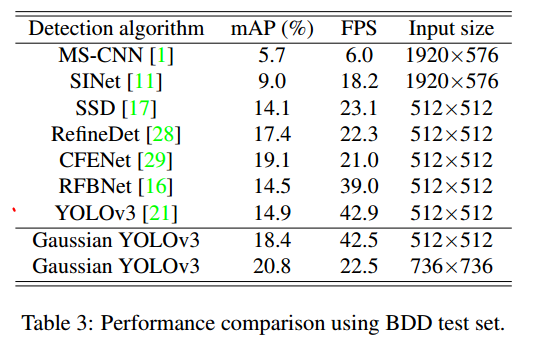
Performance




참고자료