오늘 읽은 논문은, PointNet, Deep Learning on Point Sets for 3D Classification and Segmentation 입니다.

PointNet은 3D point cloud data를 입력받아 3D shape classification, shape part segmentation, scene semantic parsing task을 수행합니다.
Properties of Point Sets
PointNet은 point cloud를 입력으로 취하며, 이 points 각각을 {x,y,z} 좌표로 나타내어 Euclidean 공간에서 다룹니다. Euclidean space에 존재하는 point들은 다음의 세가지 속성을 갖습니다.
(1) Unordere
point cloud는 unordered set of vector입니다. 따라서 신경망에 points의 순서가 무작위로 입력될 수 있습니다. 따라서 신경망은 points들이 어떠한 순서로 입력되더라도 출력값이 동일해야 합니다.
(2) Interaction among points
각 포인트들은 고립되어 있는 게 아니라, 인접 포인트와 함께 의미있는 부분집합을 형성합니다. 인접 points들은 독립 관계가 아니라 종속관계입니다.
(3) Invariance under transformation
point들은 transformation에 invariance 해야 합니다. 예를 들어, point들을 rotating 혹은 translating을 적용 하더라도 출력값이 변하면 안됩니다.
PointNet

PointNet은 목적에 따라 classification network, segmentation network로 나뉩니다. classification network는 k개의 class를 출력합니다. segmentation network는 nxm 벡터를 출력합니다. n은 포인트 갯수, m은 sub-categrory를 의미합니다.
PointNet은 3개의 핵심 모듈을 갖고 있습니다.
(1) Symmetry Function for Unordered Input

모델이 point cloud의 unordered에 invariant 하기 위해서 symmetric function을 사용합니다. symmetric function은 입력 순서에 상관없이 일정한 출력값을 생산하는 함수를 의미합니다. 그리고 symmetric function으로 max pooling을 사용합니다.
(2) Local and Global Information Aggregation
Segmentation task를 위해서 local feature와 global feature를 통합합니다. 두 정보를 concat하고, MLP를 적용하여 segmentation을 수행합니다.
(3) Joint Alignment Network
PointNet 전체 구조 그림에서 T-Net에 대한 설명입니다.

T-Net의 역할은 point cloud가 rigid transformation에 invariant를 갖기 위함입니다. rigid transformation은 rotation과 translation 변환을 의미합니다. point 간의 거리와 방향은 의미를 갖고 있으므로 이 의미가 훼손되는 것을 방지해야합니다.
PointNet은 T-Net을 사용해서 affine transformation matrix를 예측합니다. 그리고 이 matrix를 입력 point cloud에 적용합니다. 이 matrix가 point cloud에 affine transformation을 적용하여 rigid transformation에 강인해지도록 합니다.
해당 논문에서는 이 affine transformaton matrix A가 orthogonal matrix가 되도록 합니다. matrix가 orthogonal matrix가 되면 input matrix에 곱해도 도형의 원래 고유 모양이 바뀌지 않는 rigid motion이 되기 때문입니다. 이 matrix가 orthogonal matrix가 되도록 하기 위해 loss에 정규화 식을 추가합니다.
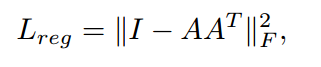
A 행렬이 orthogonal matrix이라면 AA^T는 I(identity matrix)가 됩니다. 따라서 위 손실함수를 최소화 하는 방향으로 학습을 하면 A 행렬은 orthogonal matrix가 됩니다.
Performance
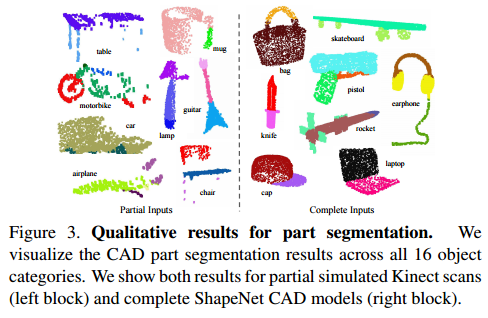



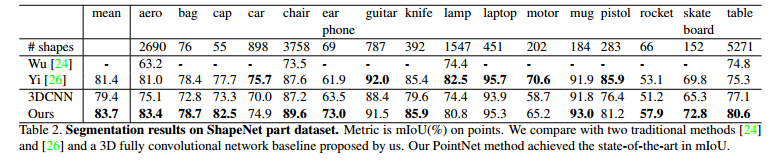
참고자료
[1] https://arxiv.org/abs/1612.00593