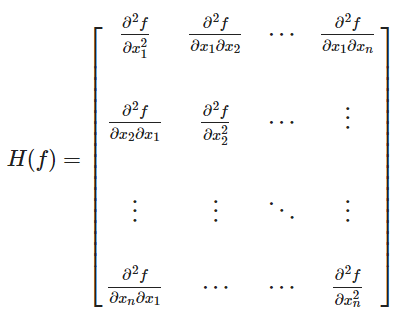해시안(Hessian) 일변수함수에서 임계점 중 극점이 되는 판별법은 f''(x0) > 0 이면 극대점, f''(x0) < 0 이면 극소점 입니다. 하지만 다변수함수에서 이계편도함수(second derivative)는 상당히 복잡합니다. 이를 위해 헤시안(Hessian)이라고 불리는 이계편도함수의 표현법을 소개하겠습니다. 이 해시안은 이차 함수(Quadratic function)과 관련이 있습니다. 다음과 같이 표현되는 경우에 이차 함수(Quadratic function)라고 합니다. 이를 행렬의 곱으로 나타내면 다음과 같습니다. 만약 3개의 변수를 받는 경우, n =3은 다음과 같습니다. 이것을 이차 함수(quadratic function)이라고 합니다. [aij]는 대칭 행렬이라고 가정합니다. 이제 ..