사이토고키의 <밑바닥부터 시작하는 딥러닝>을 공부하고 정리하였습니다.
신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는 것 입니다. 이는 곧 매개변수의 최적값을 찾는 문제이며, 이를 최적화(optimization)이라고 합니다.
1. 확률적 경사 하강법(SGD)
매개변수의 기울기를 구해, 기울어진 방향으로 매개변수 값을 갱신하는 일을 몇 번이고 반복해서 점점 최적의 값에 다가가는 것이 확률적 경사 하강법(SGD)입니다.
SGD는 수식으로 다음과 같이 쓸 수 있습니다.

여기에서 W는 갱신할 가중치 매개변수고 $\frac{\partial L}{\partial W}$은 W에 대한 손실 함수의 기울기 입니다. $\eta$는 학습률을 의미하는데, 0.01이나 0.001과 같은 값을 미리 정해서 사용합니다.
SGD는 기울어진 방향으로 일정 거리만 가겠다는 단순한 방법입니다.
파이썬으로 SGD 구현하기
calss SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads): # grads는 오차역전파로 구한 기울기입니다.
for key in params.keys():
params[key] -= self.lr * grads[key]
SGD 클래스를 사용해서 신경망 매개변수의 진행
network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
...
x_batch, t_batch = get_mini_batch(...) # 미니배치
grads = network.gradisen(x_batch, t_batch)
params = network.params
optimizer.update(parmas, grads)
...
매개변수 갱신은 optimizer가 수행하므로 optimizer에 매개변수와 기울기 정보만 넘겨주면 됩니다.
2. 확률적 경사 하강법(SGD) 단점
SGD는 단순하고 구현도 쉽지만, 문제에 따라서는 비효율적일 때가 있습니다.
SGD의 단점을 알아보고자 다음 함수의 최솟값을 구하는 문제를 생각해보겠습니다.

그래프와 등고선을 확인해 보겠습니다.

기울기를 시각화한 모습입니다.

이 기울기는 y축 방향은 크고 x축 방향은 작습니다. 여기에서 주의할 점은 최솟값이 되는 장소는 (x, y) = (0, 0)이지만, 그림이 보여주는 기울기 대부분은 (0, 0) 방향을 가리키지 않습니다.
SGD에 의한 최솟값 갱신경로를 확인해 보겠습니다.
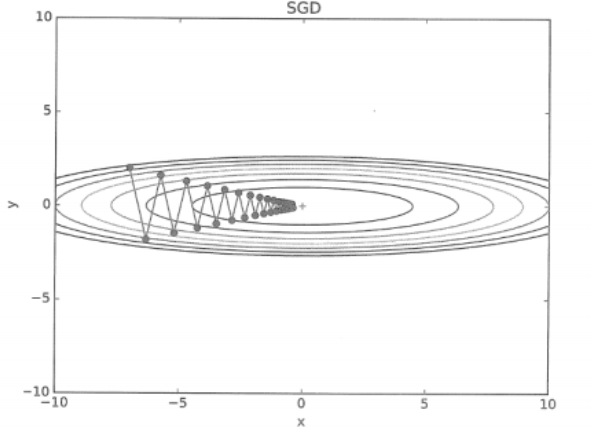
SGD는 심하게 굽이진 움직임을 보여줍니다. 상당히 비효율적인 움직임입니다.
즉, SGD의 단점은 비등방성함수(방향에 따라 성질, 기울기가 달라지는 함수)에서는 탐색 경로가 비효율적입니다.
SGD가 지그재그로 탐색하는 근본 원인은 기울어진 방향이 본래의 최솟값과 다른 방향을 가리키는 점입니다.
SGD의 이러한 단점을 개선해주는 모멘텀, AdaGrad, Adam이라는 세 방법이 있습니다.
'수학 > 딥러닝 이론' 카테고리의 다른 글
| [딥러닝] 매개변수 갱신 - AdaGrad 기법 (0) | 2020.10.02 |
|---|---|
| [딥러닝] 매개변수 갱신 - 모멘텀(Momentum) 기법 (3) | 2020.10.02 |
| 04-4 오차역전파법 (4) - 오차역전파법을 사용한 학습 구현 (0) | 2020.09.12 |
| 04-3. 오차역전파법 (3) - 활성화 함수, Affine, Softmax 계층 구현 (1) | 2020.09.12 |
| 04-2. 오차역전파법 (2) - 간단한 역전파 계층 구현 (0) | 2020.09.12 |