(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다.
(k-mooc 통계학의 이해1, 여인권)을 수강하면서 정리해보았습니다.
수치자료를 범주화하는 방법을 알아보겠습니다. 또, 범주화된 수치자료를 표나 그래프를 이용하여 정리하는 방법을 알아보겠습니다.
4. 표를 이용한 정리(수치형)
4.1 도수분포표 - frequency table
수치자료에 대한 도수분포표를 만들 때에는 관측된 값들을 몇 개의 구간으로 범주화하여 해당 그룹에 속한 관측개체의 빈도로 도수분포표를 만듭니다.
우선, 수치자료의 범주화를 알아보겠습니다.
수치자료를 범주화할 때는 몇 개의 범주로 나눌 것인지와 범주의 경계값을 얼마로 할 것인지 정해야 합니다. 자료의 특성을 고려해 분석자가 임의대로 결정할 수 있습니다.
계급(class)
각각의 범주를 의미합니다.
계급의 수
자료의 수에 비례하여 결정하는데 일반적으로 제곱근 방법, Sturges 공식, Rice 공식 등을 사용합니다.
계급의 경계
계급의 간격(크기)와 시작점과 끝점을 지정하는 것을 의미합니다. 분석자가 설명하기 쉬운 값으로 선택하여 사용합니다. 기본적으로 동일 간격이며, 자료의 구조와 설명을 고려해 선택합니다.
대부분의 자료가 특정 구간에 집중되는 경우에는 자료가 밀집된 구간을 좀더 세분화하여 범주화 해주는 것이 좋습니다.
ex) [1천만, 2천만), [2천만, 3천만), [3천만, 5천만), [5천만, 7천만), [7천만, 1억), [1억, 1억5천만]
ex) 최솟값이 7이고 최댓값이 35일때 [7, 16), [16, 25), [25,34] 와 같이 유도할 수 있지만, [5, 15), [15, 25). [25, 35] 로 폭을 10으로 만드는 것이 더 용이할 수 있습니다.
그러면 수치자료의 범주화하여 제작한 도수분포표를 살펴보겠습니다.
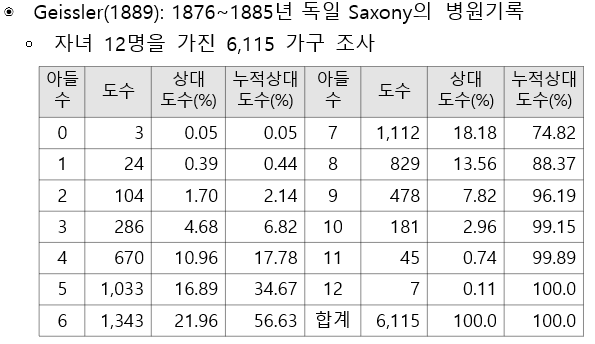
5. 그래프를 이용한 자료정리(수치형 자료)
5.1 점도표 - dot plot
각 관측값의 위치에 점을 표시하고 같은 관측값이 있는 경우 위로 누적하는 그래프입니다.

5.2 히스토그램 - histogram
히스토그램은 수치자료, 특히 연속자료가 어떤 형태로 분포되어 있는지를 알아보기 위해 사용되는데 해당 구간의 상대도수, 즉 비율을 직사각형의 면적으로 표시한 것입니다.
막대그래프와는 구간이 같다면 차이가 없고, 구간이 다르다면 차이가 존재합니다.
직사각형의 높이는 다음과 같이 구할 수 있습니다. (계급의 상대도수를 사각형의 면적으로 표시)
$$ 높이 = \frac{상대도수}{계급폭} = 밀도$$
히스토그램을 살펴보겠습니다.

5.3 줄기-잎 그림
줄기-잎 그림은 관측값의 정보를 그대로 간직하면서 자료의 분포를 알려주는 그림입니다.
줄기-잎 그림 그리기 순서
1. 자료를 순서대로 정렬
2. 줄기에는 기본단위인 10배의 값을 표시
3. 잎에는 관측값의 기본단위에 해당되는 값을 표시
그러면 줄기-잎 그림을 살펴보도록 하겠습니다.

이상으로 수치형 자료를 범주화하고, 범주화된 수치자료를 도수분포표, 점도표, 히스토그램, 줄기-잎 그림으로 나타내는 것을 알아보았습니다. 감사합니다.
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 02-5. 기술통계 (5) - 수치자료의 대체중심위치(중앙값, 절사평균, 최빈값) (0) | 2020.09.13 |
|---|---|
| [통계학] 02-4. 기술통계 (4) - 수치자료 분포의 중심위치(평균, 표본비율, 기하평균, 조화평균, 가중평균) (0) | 2020.09.13 |
| [통계학] 02-2. 기술통계 (2) - 범주형 자료 정리(도수분포표, 원도표, 막대그래프) (0) | 2020.09.13 |
| [통계학] 02-1. 기술통계 (1) - 자료의 종류와 구조(범주형, 수치형자료) (0) | 2020.09.13 |
| [통계학] 01-2. 통계학이란? (2) - 표본 추출 (단순확률, 계층, 층화, 집락추출법) (0) | 2020.09.13 |