안녕하세요! 이번에 리뷰할 논문은 'An overviw of gradient descent optimization' 입니다.
이 논문은 독자에게 optimization algorithm에 대한 직관력을 제공할 목적으로 작성했다고 합니다. optimization에 대해 이해도가 높아지면 설계한 모델에 적합한 algorithm을 선택할 수 있다고 합니다. 이해도를 높이기 위해, gradient descent의 3가지 변종을 살펴보고 해결해야 할 문제점을 제시하고 이 문제점을 해결하기 위해 제시된 8가지 algorithms(Adam, RMSprop, Adagad 등등)를 소개합니다.
경사 하강법(Gradient descent)
논문의 Introduction에 경사 하강법(gradient descent)에 대해 설명합니다.
Gradient descent는 매개 변수에 대한 비용 함수의 기울기의 반대 방향으로 매개 변수들을 갱신 함으로써, 모델의 매개 변수들로 매개변수화된 손실 함수를 최소화하는 방법이라고 설명합니다. 글로 읽어서는 이해가 잘 되지 않습니다. 그림으로 살펴보도록 하겠습니다.
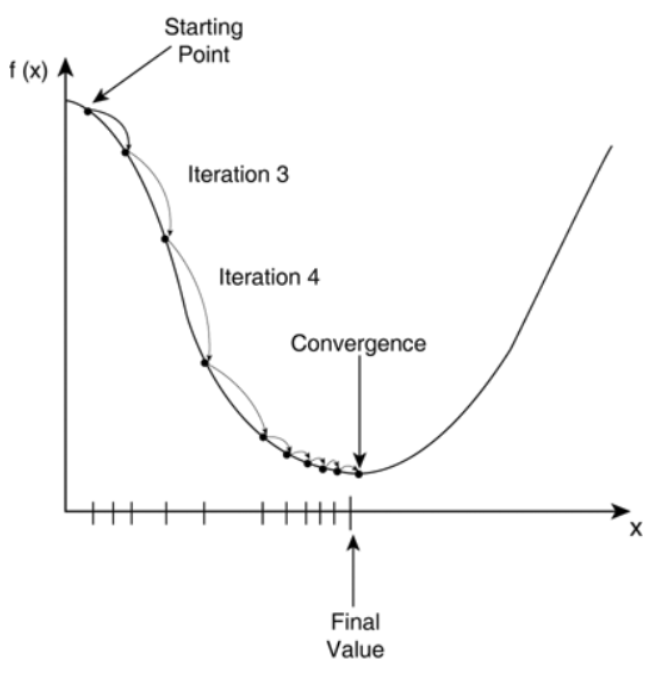
(1) 특정 파라미터 값(Starting point)으로 시작합니다.
(2) 비용 함수(Cost function)을 계산하고 starting point에서 곡선의 기울기를 계산합니다.
(3) 파라미터 값을 업데이트 합니다.(Wnew = W - learning rate * dW)
(4) 위 과정이 n번의 iteration으로 진행되고, 최소값(Final Value)을 향하여 수렴(Convergence)합니다.
즉, 경사 하강법은 비용 함수로 생성된 평면의 기울기의 방향으로 평평한 곳까지 도달할 때 까지 서서히 내려가는 것입니다.
learning rate에 대해서도 설명하는데, learning rate는 최소값에 도달하기 위한 step size를 결정한다고 합니다. iteration마다 어느 정도 하강할 것인지 결정하는 hyper parameter 입니다. 다른 말로 하면 매개 변수를 어느 정도 크기로 갱신할 것인지 결정합니다. 값이 너무 크면 매 iteration마다 큰 범위로 이동하므로 수렴하기가 어려워지고, 값이 너무 작으면 수렴하는데 시간이 너무 오래 걸립니다. 따라서 적절한 값을 설정해주는 것이 중요합니다.
다양한 경사 하강법(Gradient descent variants)
논문에서 3가지 경사 하강법에 대해 설명합니다. 이들은 손실 함수의 기울기를 계산하기 위해 얼마나 많은 데이터를 사용하는지에 따라 다르다고 합니다.
1. Batch gradient descent
전체 training dataset으로 매개 변수에 대한 비용 함수의 기울기를 계산합니다.

$\theta$는 파라미터, $\eta$는 학습률, $\triangledown$은 미분을 의미합니다.
단점은 전체 dataset으로 기울기를 계산하여 한 번에 매개 변수를 갱신하기 때문에 (1) 매우 느리고, (2) memory에 적합하도록 dataset을 다루기가 어렵습니다. 또, non-convex surface에서 local minimum에 빠지면 벗어나기 어렵습니다. 또, batch gradient descent는 전체 dataset으로 기울기를 계산하기 때문에 불필요한 연산을 수행한다고 합니다.
2. Stochastoc gradient descent(SGD)
SGD는 각 training example에 대해 매개변수를 갱신합니다.

SGD는 하나의 data로 매개변수를 한번 갱신하므로 불필요한 연산을 버린다고 합니다. 그러므로 빠르고 online에서 학습하기 위해 이용될 수 있습니다. SGD는 높은 편차로 빈번하게 갱신을 수행하므로 아래 그림과 같이 비용 함수가 크게 변동합니다.

크게 변동한다는 것은 어떤 의미를 지니고 있을 까요?
첫 번째는 local minimum에 빠졌을 때 큰 변동으로 이를 빠져나오고 새로운 local minimum을 찾을 수 있다는 것을 의미합니다. 두 번째는 크게 변동하므로 정확한 값에 수렴하기가 어렵다는 것을 의미합니다. 하지만 이는 learning rate를 천천히 낮춰 주어 수렴하도록 할 수 있습니다.
3. Mini-batch gradient descent
Mini-batch gradient descent는 우리가 일반적으로 말하는 SGD를 의미합니다. Mini-batch gradient descent는 이름 그대로 n개의 training examples로 묶인 Mini-batch에 대하여 기울기를 계산하고 매개변수를 갱신합니다.
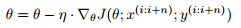
이 방법으로 (1) 더 안정한 수렴을 이끌 수 있도록 매개변수 갱신의 분산을 감소시킵니다. (2) mini-batch에 대해 고도로 최적화된 matrix를 사용하여 딥러닝 프레임워크를 사용할 수 있기 때문에 비용 함수의 기울기를 효율적으로 계산할 수 있습니다.
Challenges
위에서 알아본 경사하강법은 좋은 수렴을 보장하지 않습니다. 해결되어야 할 몇 가지 도전과제를 설명합니다.
- 적절한 learing rate를 선정하는 것은 어렵습니다. learning rate가 너무 작으면, 수렴하는데 오랜 시간이 필요합니다. 반대로 너무 크면, 최소값 근처에서 변동하거나 심지어 벗어날 수 있어 수렴을 방해합니다.
- Learning rate schedule을 사용하여 학습 도중 learning rate를 조정할 수 있습니다. 사전 정의된 schedule에 따라 learning rate를 감소시키거나, 매 epoch마다 loss가 임계값 아래로 떨어지면 learning late를 감소시키는 방법이 있습니다. 하지만 이 두 방법은 사전에 정의해야 하며, dataset의 특성에 적응될 수 없습니다.
- 동일한 learning rate가 모든 매개변수 갱신에 적용됩니다. 만약 data가 sparse하고 features가 매우 다른 빈도수를 지니고 있으면, 이 모든 것들을 동일한 정도로 갱신하면 안됩니다. 드물게 발생하는 feature에 대해서는 큰 갱신을 수행해야 합니다.
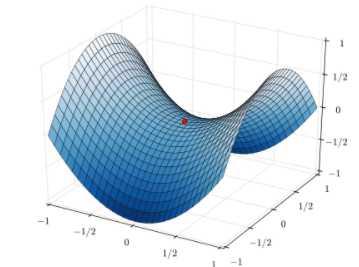
- 최적이 아닌 (국소 최적값)local minima와 안장점(saddle point) 빠질 위험이 있습니다. 안장점은 평면으로 둘러싸여 있으므로 기울기가 0인 지점을 의미합니다. 안장점이 최소값이 아니더라도 0의 기울기를 지니고 있으면, 매개변수는 갱신되지 않습니다.
경사 하강법 최적화 알고리즘(Gradient descent optimization algorithms)
위에서 설명한 도전과제들을 해결하기 위해 사용되는 몇가지 알고리즘을 소개하겠습니다.
1. Momentum
SGD는 기울기가 높은 평면에서 최적값을 향해 잘 찾아가지 못합니다. 아래 그림처럼 경사도의 기울기를 따라 왔다갔다 하는 것을 확인할 수 있습니다.

Momentum은 최적값의 방향으로 SGD가 가속하도록 도와주고 위 그림에서 보이는 진동을 완화시키는 방법입니다. 논문에서 나와있는 수식은 다음과 같습니다.

SGD 수식에서 모멘텀 항인 $\gamma v_{t-1}$를 추가적으로 빼주는 것을 확인할 수 있습니다.
이 변수가 내리막길에서는 가속하도록 도와주고, 방향이 바뀌었을 때 파라미터가 갱신하는 양을 감소시킵니다.
관성을 생각하면 이해하기가 편합니다. 수식에 모멘트를 추가하여 이전에 이동하는 방향과 크기를 현재 갱신 값에 영향을 줍니다. 이 덕분에 이동하는 방향으로 계속 이동하려하는 관성이 추가된 것입니다. 빠르게 이동하는 자동차가 갑자기 방향을 바꾸기 어렵듯이, SGD에 관성을 추가하여 갑자기 방향을 바꾸기 어렵게하고 이전과 동일한 방향으로 나아갈 때는 가속이 작용되도록 합니다.
2. Nesterov accelerated gradient(NAG)
NAG는 멈춰야할 시기에 더 나아가지 않고 제동을 거는 방법입니다.
NAG는 비용 함수의 기울기를 계산할 때, 매개변수에 이전 모멘텀을 빼주어 다음 위치를 근사화하여 비용함수의 기울기를 계산합니다. 즉, 현재 파라미터로 기울기를 계산하는 것이 아니라 파라미터의 다음 위치의 근사치로 기울기를 계산하는 것입니다. 다른 말로하면, 이전에 계산된 모멘텀항에서 다음 매개변수의 위치를 예측합니다.
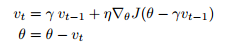
Momentum 방법과 비교하여 도식화하면 다음과 같습니다.
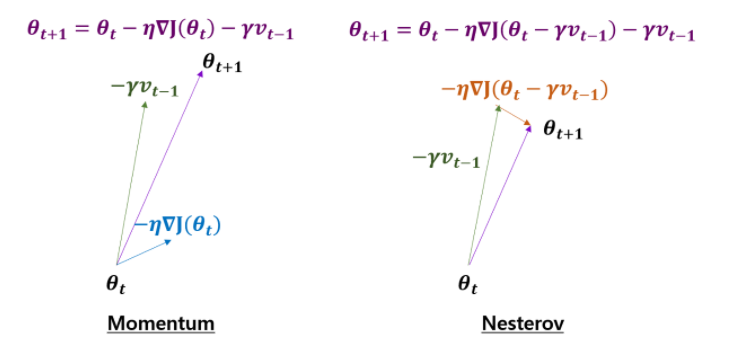
Momentum은 현재 기울기를 계산하고 모멘텀을 적용시켜 그 방향으로 크게 이동합니다. NAG는 Momentum 위치에서 다음 위치를 예측하여 파라미터를 갱신합니다. 그림에서 보듯이 NAG는 Momentum과 비교하여 보면 상대적으로 느린 속도로 값이 갱신된다는 것을 확인할 수 있고, 너무 빠르게 기울기가 수정되는 것을 방지할 수 있습니다. 그리고 NAG는 RNN의 성능을 크게 증가시켰다고 말합니다.
지금까지 알아본 알고리즘은 손실 함수의 기울기로 갱신을 하였고, SGD의 속도를 향상시켰습니다. 이제 매개변수의 중요성에 따라 각각의 매개변수에 가중치를 두어 갱신을 하는 알고리즘에 대해 알아보도록 하겠습니다.
3. Adagrad(Adaptive subgradients)
Adagrad는 다음과 같은 방식으로 작동하는 gradient-based optimization 입니다. 빈번하게 등장하는 매개변수는 적게 갱신하고 드물게 등장하는 매개변수는 크게 갱신합니다. 모든 매개변수가 동일하게 갱신되는 것이 아니라 매개변수의 빈도수에 따라 가중치를 부여하여 갱신합니다. 이러한 이유로 sparse data를 다루기 위해 매우 적합합니다. 또한 SGD의 견고성을 크게 향상시켰다고 말합니다.
이전까지 모든 매개변수는 동일한 학습률(learning rate)을 사용하여 갱신했습니다. Adagrad는 매번 각각의 매개변수에 서로 다른 학습률을 사용합니다.
Adagrad에 이용되는 수식을 알아보겠습니다.

각각의 매개변수에 서로 다른 학습률이 적용되므로 새로운 기호인 $\theta_{t,i}$가 나타납니다.
t는 time step, i는 개별 매개변수를 의미합니다.
그리고 비용 함수의 기울기를 $g_{t,i}$로 표현합니다.

그리고 $G_{t,ii}$는 대각 요소가 t시점 까지의 각 매개변수의 기울기의 제곱합입니다. $\epsilon$은 분모가 0이 되는 것을 방지하기 위한 아주 작은 숫자입니다.
$G_t$는 대각 행렬이고, 대각 요소가 모든 매개변수에 대한 비용 함수의 기울기의 제곱 합으로 이루어져 있으므로 elementwise matrix vector 곱을 이용하여 정리할 수 있습니다.

Adagrad의 장점은 학습률을 수동으로 조정할 필요가 없다는 것입니다. 초기 학습률을 0.01으로 설정하고 이것을 이대로 냅둡니다. $G_t$가 자동으로 학습률을 조정해주기 때문입니다.
Adagrad의 단점은 분모에 제곱된 기울기가 계속 축적된다는 것입니다. 모든 항이 양수이면 training 동안 계속 값이 커질 것입니다. 이것은 학습률이 점점 줄어들게 하고 결국 학습률은 매우 작게 될것입니다. 따라서 알고리즘은 추가적인 정보를 획득하지 못하게 됩니다.
다음에 배울 Adadelta는 Adagrad의 단점을 보완한 방법입니다.
4. Adadelta
Adadelta는 Adagrad의 확장된 버전입니다. Adagrad는 시간이 지날수록 학습률이 단순 감소하게 됩니다. Adadelta는 과거의 모든 기울기를 이용하지 않고 특정한 구간의 기울기만을 이용합니다.
비효율적으로 이전의 제곱된 기울기를 저장하여 평균을 계산하지 않고, 이전에 제곱된 기울기의 이동 평균을 이용하여 평균을 계산합니다. 가중 평균$E[g^2]_t$는 t 시점에서, 단지 이전까지의 평균과 현재 기울기만을 이용합니다.

$\gamma$는 보통 0.9로 설정합니다.
위 수식에서 볼 수 있듯이 이동 평균을 이용하는 모습입니다. 이전 시점까지의 평균값의 0.9비율과 갱신될 제곱된 기울기 0.1 비율을 더해주어 평균을 계산합니다.
Adadelta에서는 매개변수의 변화량 $\triangle$을 이용하여 수식을 표현합니다. 아래는 SGD에서의 수식을 매개변수 변화량으로 표기한 것입니다.

Adagrad에서는 매개변수 변화량은 다음과 같습니다.

이제 이동 평균을 이용하는 Adadelta에서 매개변수 변화량은 다음과 같습니다.
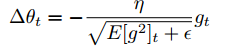
분모가 기울기의 root meat squared(RMS)이므로 다음과 같이 표현할 수 있습니다.

Adadelta 논문 저자는 SGD, Momentum, Adagrad, Adadelta에서 이 업데이트 단위가 일치하지 않는 다는 문제점이 있다고 말합니다. 이를 해결하기 위해 또 다른 가중 평균을 정의합니다. 제곱된 기울기가 아니라 제곱된 매개변수를 이용하여 갱신합니다.

따라서 매개변수의 root mean squared는 다음과 같이 정리됩니다.

최종적으로 매개변수의 변화량을 이용해서 Adadelta 식을 정리하겠습니다.

Adadelta는 학습률을 설정할 필요가 없습니다. 수식에서 학습률이 제거됬기 때문입니다.
5. RMSprop
RMSprop는 publish된 논문이 따로 있지 않고, Geoff Hinton의 코세라 강의에서 제안된 방법입니다.
RMSprop와 Adadelta는 Adagrad의 학습률이 소실되는 문제를 해결하기 위해 발전되었습니다. RMSprop는 Adadelta의 첫 번째 수식과 동일합니다.

$\gamma$ = 0.9, 학습률($\eta$) = 0.001로 제안합니다.
6. Adam(Adaptive Moment Estimation)
Adam(Adaptive Moment Estimation)은 각각의 매개변수에 학습률을 다르게 계산하는 또 다른 방법입니다. Adadelta와 RMSprop와 같이 과거의 제곱된 기울기 $v_t$의 지수적으로 감소하는 가중 평균을 적용할 뿐만 아니라, Momentum과 비슷하게 과거의 기울기 $m_t$의 지수적으로 감소하는 가중 평균을 적용합니다.

$m_t$는 기울기의 1차 모멘트(평균)의 추정량이고 $v_t$는 기울기의 2차 모멘트(분산)의 추정량 입니다.
$m_t$와 $v_t$는 0으로 초기화 되기 때문에, 학습 초기때와 decay rate($\beta_1, \beta_2$가 1에 가까울 때)가 매우 작을 때 이들은 0으로 편향되어 있습니다. 이를 해결하기 위해 편향이 수정된 1차 모멘트와 2차 모멘트의 추정값을 이용합니다.

다음과 같이 수정함으로써 초기에 0으로 편향되어 있는 것을 예방할 수 있습니다.
Adam은 위 수식을 Adadelta와 RMSprop에서 보았던 매개변수 갱신에 사용합니다.
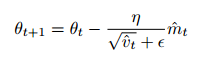
즉, $\hat{m_t}$는 momentum 역할을 수행하고, $\hat{v_t}$는 각각 파라미터에 서로 다른 학습률을 적용하는 역할을 합니다.
논문에서는 $\beta_1$ = 0.9, $\beta_2$ = 0.999, $\epsilon$ = $10^{-8}$을 제안합니다.
7. AdaMax
Adam에서 $v_t$를 계산할 때, $v_{t-1}$항과 현재 기울기의 $l_2$ norm을 이용합니다.
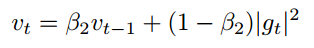
$l_2$ norm을 $l_p$ norm으로 확장할 수 있습니다.

p가 큰 값을 가지면 수치적으로 불안정해지므로 보통 $l_1$ norm, $l_2$ norm을 이용합니다.
하지만 p = $\infty$ 일때, $l_{\infty}$ norm은 좀 더 안정적으로 수렴한다고 합니다.
Adam과 혼동을 피하기 위해 $v_t$대신 $u_t$를 사용하여 표기하겠습니다.
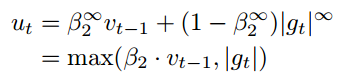
이처럼 $u_t$는 max 연산에 의존하므로 Adamax라는 이름이 붙여졌습니다.
또한 max 연산이므로 $m_t$와 $v_t$가 0에 편향을 지니지 않습니다.
최종 수식은 다음과 같습니다.

8. Nadam
지금까지 살펴본 optimization을 복습해보도록 하겠습니다. Adam은 RMSprop와 momentum의 결합으로 볼 수 있습니다. RMSprop는 제곱된 기울기 $v_t$의 가중 평균을 이용하였고, momentum은 기울기 $m_t$의 가중 평균을 이용하였습니다. Nesterov accelerated gradient(NAG)는 SGD보다 성능이 더 좋았습니다.
Nadam(Nesterov-accelerated Adaptive Moment Estimation)은 Adam과 NAG가 결합된 것입니다. NAG를 Adam으로 통합시키기 위해서 momentum항인 $m_t$를 수정해야 합니다.
첫 번째로, momentum update rule을 복습해보겠습니다.

여기서 J는 비용함수이고, $\gamma$는 momentum decay term, $\eta$는 학습률 입니다. 이는 다음과 같이 표현할 수 있습니다.

이 수식은 이전의 momentum vector와 현재 기울기의 방향을 고려합니다.
NAG는 기울기를 계산하기 전에 momentum을 매개변수에 빼주어 $g_t$를 계산하기 때문에, 기울기 방향으로 더 정확하게 나아갈 수 있습니다. 따라서 NAG 처럼 $g_t$를 수정하면 됩니다.

Dozat는 다음의 방법으로 NAG를 수정하는 것을 제안합니다. momentum step을 두 번 적용(한번은 기울기 $g_t$를 갱신할 때, 두 번째는 매개변수 $\theta_{t+1}$을 갱신할 때)하는 것보다 현재 매개변수를 갱신하기 위해 직접적으로 현재의 momentum vector를 적용할것입니다.

매개변수를 갱신할 때 $m_{t-1}$이 아닌 $m_t$를 적용했습니다. Adam에 Nesterov momentum을 적용시키기 위해 이전 momentum vector를 현재 momentum vector로 바꿔주면 됩니다.
최종적으로 Nadam 식은 다음과 같이 정리할 수 있습니다.

알고리즘의 시각화(Visualization of algorithms)



그림에서 보면 상황에 따라 빠르게 수렴하는 알고리즘이 다른것을 확인할 수 있습니다.
그러면 어떤 알고리즘을 선택해야 할까요??
SGD는 minimum을 찾지만 최적화하는데 상당히 오래 걸리고 초기치와 learning rate schedule에 크게 의존한다고 합니다. 그리고 saddle points에 갖힐 확률이 높다고 합니다. 따라서 논문에서는 adaptive learing rate methods 중에 하나를 선택하라고 합니다.
Conclusion
이 논문에서 3가지의 gradient descent를 살펴보았고, SGD를 최적화하기 위해 흔하게 사용되는 알고리즘(SGD:momentum, NAG, Adagrad, Adadelta, RMSprop, Adam, AdaMAx, Nadam)을 조사해보았습니다. 이 논문에는 Optimization 이외에 SGD를 향상시키는 또 다른 전략(shuffling, curriculum learning, batch normalization, early stopping)을 짧게 소개합니다. 관심 있으신 분들은 논문을 읽어 보시는 것을 추천드립니다. 읽어주셔서 감사합니다.
참고자료
[2] bioinformaticsandme.tistory.com/125
[3] ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95
[5] shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html
'논문 읽기 > Optimization' 카테고리의 다른 글
| [논문 읽기] AdamW(2017), Decoupled Weight Decay Regularization (0) | 2021.07.14 |
|---|