[논문 읽기] AdamW(2017), Decoupled Weight Decay Regularization

 안녕하세요, 오늘 읽은 논문은 AdamW(2017), Decoupled Weight Decay Regularization 입니다.

 

핵심 정리

 weight decay는 loss function에 L2 regularization를 추가하여 구현할 수 있으며 딥러닝 라이브러리가 optimization 함수에 동일한 방법으로 적용되어 있습니다. SGD의 경우에는 weight decay = L2 reg 가 성립하지만 Adam의 경우에 파라미터마다 학습률을 다르게 적용하여 L2 reg로 weight decay를 구현한다면 동일하지 않아 성능이 하락합니다. 이 문제를 해결하기 위해 weight decay를 분리하여 따로 구현합니다.

 

Motivation

 여러 task에 test를 진행할때, SGD with momentum이 adaptive gradient method인 Adam보다 좋은 generalization을 보여줄 때가 있습니다. 따라서 연구자들은 SGD, Adam 각각에 대하여 선택 고민과 실험을 해야 합니다. 논문 저자는 Adam이 SGD with momentum보다 worse generalization을 보여주는 task에 대해서도 Adam이 competitive 하도록 만드는 것이 main motivation 입니다.

 

Problem

 특정 task에서 Adam의 worse generalization는 (1) presence of sharp local minima, (2) inherent problems of adaptive gradient method 에 의해 발생한다고 가설을 세웁니다. 그리고 저자는 딥러닝 라이브러리에서 weight decay 방법으로 Adam의 알고리즘 내부에 구현되어 있는 L2 reguralization이 SGD보다 덜 효과적이기 때문에 poor generalization이 발생한다고 말합니다.

 

 저자는 Adam을 분석하여 다음과 같은 관측을 합니다.

 

(1) L2 reguraization and weight decay are not identical

 weigt decay는 SGD에서 L2 reguralization으로 구현되어 있고 이는 Adam에서 weight decay = L2 regularization 이 성립되지 않습니다. Adam에서 L2 reguralization을 weight decay로 구현하는 경우에 weight decay를 사용하는 것보다 파라미터와 gradient 크기가 더 적게 regularization 된다고 합니다.

 

(2) L2 regularization is not effective in Adam

 딥러닝 라이브러리는 original weight decay가 아니라 L2 regularization으로 구현되어 있습니다. 이 L2 reg는 SGD에만 효과적이며 Adam의 경우에 worse result를 보입니다.

 

(3) weight decay is eqully effective in both SGD and Adam

 weight decay는 SGD와 Adam에 모두 효과적이지만 L2 reg는 SGD에서만 효과적입니다.

 

(4) Optimal weight decay depends on the total number of batch passes/weight updates

 large number of batch 를 사용하는 경우에 optimal weiht decay는 작아집니다.

 

(5) Adam can substantially benefit from a scheduled learning rate multiplier

 각 파라미터에 대해 서로 다르 learning rate를 적용하는 Adam은 global learning rate multiplier scheduler(ex, cosine annealing)를 사용하여 상당한 성능 개선을 이뤄낼 수 있습니다.

 

Contribution

 Adam에서의 gradient-based update(optimization step)로부터 weight decay를 decouple하여 regularization 효과를 개선합니다. 논문에서 제안하는 decoupled weight decay는 learning rate의 optimal seting과 weight decay factor를 더 independent하게 만듭니다. 따라서 하이퍼파라미터 최적화가 쉬워집니다.

 

Method

 gradient based update에서 weight decay를 분리합니다. 왜 분리할까요? Adam에서 weight decay와 L2 regularization이 동일하지 않기 때문입니다.

 

 SGD에서는 L2 regularization과 weight decay가 동일하게 구현될 수 있습니다.

 

 일반적으로 L2 regularization은 손실함수에 다음과 같이 적용됩니다.

 

 

 이를 미분하여 그래디언트를 계산하고 파라미터를 갱신합니다.

 

 

 weight decay 를 적용한 식은 다음과 같습니다.

 

 

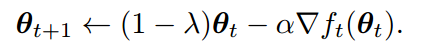
 이처럼 손실함수에 L2 reg를 적용하면 weight decay도 자동으로 적용되기 때문에 많은 프레임워크에서 weight decay를 L2 reg로 구현합니다. 하지만 이는 Adam에서 성립되지 않습니다. 또한 $\lamda$'는 = weigt decay factor / lr 이므로 최적의 lr을 찾았다 하더라고 weight decay factor가 변경되면 다시 최적의 lr을 찾아야 합니다. 논문에서 제안하는 AdamW는 두 factor을 independent 하도록 분리합니다.

 

 Adam의 경우에 weight decay가 없는 손실함수로 gradient update를 하면 다음과 같습니다.

 

 

 loss function에 L2 reg를 적용하고 미분하여 update 하는 식

 

 

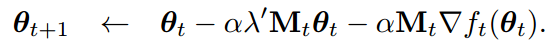
 weight decay를 적용하면 다음과 같은 식이 도출되는데 이는 M != KI 이므로 loss function에 L2 reg를 적용한 식과 다릅니다.

 

 

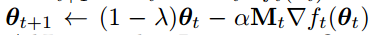
 따라서 다음과 같이 weight decay를 분리한 알고리즘 AdamW를 제안합니다.

 

 

 SGD에서는 L2 reg와 weight decay 모두 동일한 비율로 weight를 0으로 축소시킵니다. 하지만 Adam에서는 손실 함수의 기울기가 adaptive 하게 적용되므로 동일한 비율로 weight를 축소시키지 않습니다. 따라서 weight decay 단계를 분리하여 구현합니다.

 

Experiment

 Adam, AdamW 두 가지 optimization을 fixed lr, lr decay, cosine lr 3가지 조건에서 test error를 비교합니다. AdamW + cosine lr 이 가장 test error가 낮습니다. 데이터셋은 CIFAR-10, 100 epoch 입니다.

 

 Adam, AdamW, SGD, SGDW 비교

 

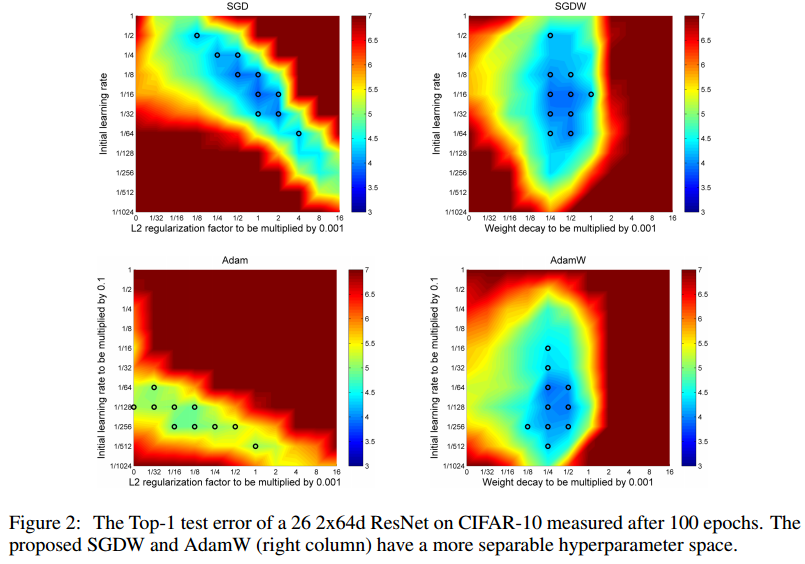
 학습곡선, Loss, test error 분석

 

 Cosine annealing이 아닌 warm restart를 적용한 AdamWR, SGDWR

 

---

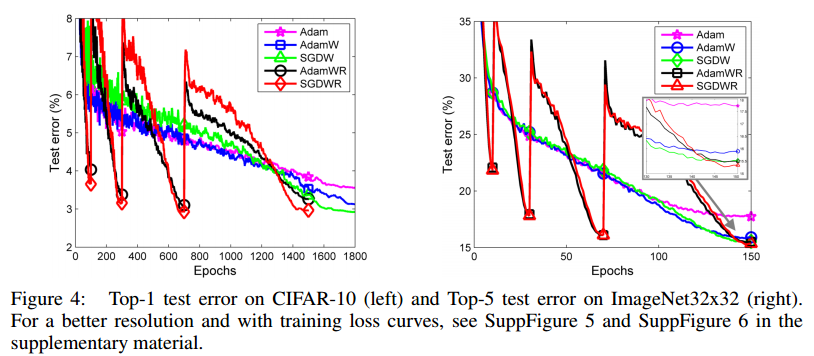
참고자료

[1] https://arxiv.org/abs/1711.05101