[논문 리뷰] 배치 정규화, Batch Normalization(2015)

 

 안녕하세요! 이번에 리뷰할 논문은 'Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift' 입니다!

 

 배치 정규화는 2015년에 제안된 방법입니다. 배치 정규화는 많은 사람들이 사용하고 있으며, 주목 받는 이유는 다음과 같습니다.

 

• 학습을 빠르게 진행할 수 있습니다.(높은 학습률을 적용 가능합니다)
• 초깃값에 크게 의존하지 않습니다.(초깃값 선택 장애를 개선했습니다)
• 오버피팅을 억제합니다.(드랍아웃의 필요성을 감소했습니다.)
• 비선형 함수(sigmoid 등)을 이용할 때, saturated regime(기울기가 0인 부분)에 빠지는 것을 방지합니다. 따라서 기울기 소실과 saturation problem을 예방합니다.

 

 이처럼 엄청난 효과를 갖고 있는 배치 정규화는 각 층이 활성화를 적당히 퍼뜨리도록 '강제'해보자는 아이디어에서 출발했는데요. 어떻게 활성화를 퍼뜨리고 위의 효과를 낼 수 있는지 알아보도록 하겠습니다!

 

---

내부 공변량 변화(Internal Covariate Shift)

 배치 정규화는 내부 공변량을 감소시키기 때문에 학습속도를 높일 수 있다고 설명합니다. 그러면 내부 공병량이 무엇인지 알아보도록 하겠습니다.

 

 참고로 2017년 배치 정규화 후속논문에서 배치 정규화가 좋은 성능을 나타내는 이유는 내부 공변량 변화와는 관계가 없고 optimization에 smoothing 효과를 주기 때문이라고 합니다. 관심이 있으신 분은 'SANTURKAR, Shibani, et al. How Does Batch Normalization Help Optimization?' 를 읽어보시길 추천드립니다.

 논문에서는 Internal Covariate Shift를 학습 도중 신경망 파라미터 변화에 의한 신경망 activation의 분포의 변화라고 정의합니다. 그리고 이 Internal Covariate Shit를 감소시켜야 학습을 개선할 수 있다고 말합니다. 아래 그림 처럼 신경망이 깊어 짐에 따라 activation의 분포가 바뀌어 가는 것입니다.

 

 

 internal covariate shift는 각 층마다 입력값의 분포가 변하게 되는 것으로도 생각해 볼 수 있습니다.

 

 internal covariate shift가 발생하게 되면 어떤 단점이 존재할까요??

 

---

내부 공변량 변화(internal covariate shift)의 단점

 단점으로는 다음과 같습니다.

• saturated regime(활성화 함수에서 기울기가 0인 부분)에 빠지고 기울기 소실 및 폭발이 발생합니다.

 위 단점은 ReLU 함수를 이용하거나 신중한 초기값 선택, 적은 학습률을 적용하여 문제를 해결할 수 있습니다.

 

 하지만 적절한 초깃값을 이용하는 것은 어려운 일이며, 적은 학습률을 적용하게 되면 학습 속도가 느려지게 됩니다. 내부 공변량 변화 문제를 해결한다면 초깃값에 대한 의존도를 낮출 수 있고, 높은 학습률을 적용하여 학습속도도 빨라지며 기울기 소실 및 폭발 문제도 해결할 수 있는 것입니다.

 

 그러면 어떻게 내부 공변량 변화의 문제를 해결할 수 있을 까요?

 

---

내부 공변량(internal covariate)를 감소시키는 방법

논문에서는 whitening 기법을 설명합니다. whitening을 매 hidden layer의 입력값에 적용을 하면 고정된 분포를 갖게 되어 internal covariate shift의 영향을 감소시킨다고 말합니다.

 

 하지만 whitening 기법을 적용하게 되면 연산량이 너무 많아지고 backpropagation에서 문제가 생긴다고 말합니다. 그래서 2가지 간소화(simplication)을 적용해야 한다고 말합니다.

 

 우선 whitening 기법이 무엇인지 알아보도록 하겠습니다.

 

whitening 기법

 whitening은 평균 0, 분산 1, decorrelated 해주는 선형 변환을 의미합니다. 각 layer의 입력값에 whitening을 적용시키면 internal covariate shift를 감소시킬 수 있을 것이라고 말합니다. 하지만 문제점이 있었습니다.

 

whitening 기법 문제점

• covariance matrix 계산과 inverse 계산이 필요하기 때문에 계산량이 많습니다.
• whitening을 하면 일부 파라미터들의 영향이 무시되어 gradient descent 효과를 감소시킵니다.

 whitening 기법을 매 layer 입력값에 적용하면, optimization 단계에서 문제가 생겨 gradient descent의 효과를 감소시킨다고 말합니다.

 

 왜 gradient descent의 효과를 감소시키는 것일까요?

 

 layer의 입력 u에 편향 b를 더한 것을 x 라고 하겠습니다. (x = u + b). 여기에 평균을 빼주어 normalize를 합니다. (x - E[x]). 평균값을 빼주는 과정에서 b도 같이 빠지게 되어 결국 출력에서 b의 영향이 없어진다고 논문에서 설명하고 있습니다. 만약 표준 편차로 나누거나 scaling 과정까지 하게 된다면 이 문제점은 더 약화된다고 합니다.

 

 

 각 layer의 입력을 모두 whitening 하는 것은 많은 계산량이 필요하고, 모든 곳에서 미분이 가능하지 않기 때문에 두 가지 간소화를 해야한다고 말합니다. 어떻게 간소화를 하고 위 문제점을 해결했는지 알아보도록 하겠습니다.

 

---

문제점을 해결하기 위한 두 가지 간소화(Simplication)

 각 layer의 입력에 whitening을 해주어 internal covariate shift를 감소시키는 방법은 두 가지 문제점이 있었습니다. 이 문제점을 해결하기 위해 두 가지 방법을 이용합니다.

 

첫 번째 방법

 layer의 입력과 출력을 동시에 whitening 해주는 대신에 각 scalar feature을 평균 0, 분산 1을 갖도록 독립적으로 normalize 해줍니다.

 

 

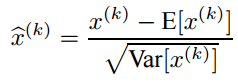
 이러한 normalize는 feature가 decorrelated 되지 않았음에도 수렴 속도를 높여준다고 합니다.

 

 위의 normalize는 단점이 있었습니다.

 

 sigmoid의 입력을 위와 같이 normalize 하는 것은 nonlinearity의 linear regime로 제한하게 됩니다. 따라서 비선형성을 읽게 되는 것 입니다. 

 

 

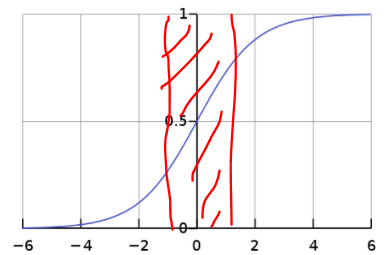
 위의 표시된 영역에만 입력이 존재하게 되어 비선형성을 잃게 됩니다.

 

 이를 해결하기 위해 normalize된 값을 scale, shift 해주는 학습 가능한 파라미터 감마와 베타를 추가합니다.

 

 

 평균 0, 분산 1로 normalized된 값을 감마와 베타로 scale, shift 해준다면 sigmoid의 선형 구역을 벗어날 수 있게 됩니다.

 

두 번째 방법

 normalize는 전체 dataset을 처리하지만 SGD는 batch 단위로 데이터를 처리합니다. 따라서 SGD를 이용하게 되면 전체 dataset을 normalize하는 것은 비현실적이게 됩니다. 따라서 normalize도 batch 단위로 해줍니다.

 

 각각의 mini-batch data로 layer의 입력을 normalize 해줍니다. 이 방법으로 normalization에 사용된 통계값은 모두 backpropagation에 참여할 수 있습니다. normalize를 mini-batch 단위로 처리하게 되면 한번에 처리하는 연산량도 줄어들게 되는 이점이 있습니다.

 

최종 수식

  최종적으로 배치 정규화 수식은 다음과 같이 됩니다.

 

 

 이 과정을 통해서 학습 동안 각 층의 activation 값들이 안정적인 분포를 갖게 되는 것입니다.

 

---

참고 자료

[1] ucsd.tistory.com/39

[2] blog.naver.com/PostView.nhn?blogId=laonple&logNo=220808903260