안녕하세요, 오늘 읽은 논문은 CBN, Cross-Iteration Batch Normalization 입니다.
CBN은 small batch size에서 발생하는 BN의 문제점을 개선하기 위해 이전 Iteration에서 사용한 sample 데이터로 평균과 분산을 계산합니다. 현재 가중치와 이전 가중치가 다르기 때문에 단순하게 이전 Iteration 에서 사용된 sample을 활용하면 추정된 통계값이 부정확 하여 성능에 악영향을 줍니다. CBN은 테일러 시리즈를 사용해 이전 가중치와 현재 가중치의 차이만큼 compensation하여 근사화 합니다. 매 반복마다 변화하는 가중치 값이 매우 작다고 가정하기 때문에 테일러 시리즈를 사용할 수 있습니다.
Batch Normalization(BN)
BN은 딥러닝에서 필수적으로 사용하는 기법입니다. 신경망의 파라미터의 갱신 때문에 학습 과정동안 활성화 함수의 분포가 계속해서 변화합니다. 이는 성능에 악영향을 주며 기울기 소실을 유발할 수 있습니다. BN은 활성화 함수 입력값을 평균과 분산으로 normalization하여 이 문제를 완화합니다.
BN을 잠깐 살펴보겠습니다.
BN은 mini-batch 안에 존재하는 sample들로 평균과 분산을 계산합니다. BN은 각 batch로 계산한 통계값이 전체 training set과 일치한다고 가정합니다. 이 가정은 large batch size에는 유효하지만, small batch size에서는 유효하지 않습니다.


계산한 평균과 분산으로 값을 whitening을 진행합니다. whitening은 값의 분포가 0 평균, 1 분산을 갖도록 하는 방법입니다. v는 E(x^2)를 의미합니다.

whitening 된 값에 학습 가능한 파라미터 감마와 베타를 갖도록 선형 변환을 수행합니다.
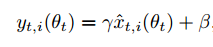
whitening된 x 값을 감마와 베타로 shift하여 다양한 일정한 기울기 값을 갖도록 합니다.
BN의 문제점
BN의 문제점은 mini-batch size가 작은 경우에 발생합니다. 적은 sample로 평균과 분산을 추정하므로 추정된 값은 전체 training set과 동일하지 않습니다. 따라서 많은 noise가 포함되고 이는 성능에 악영향을 주게 됩니다.
모든 상황에서 large batch size를 사용한다면 BN은 문제가 되지 않습니다. 하지만 많은 연산량과 메모리 점유율이 필요한 object detection, segmentation task에서는 GPU 한계 때문에 작은 batch-size를 사용할 수 밖에 없습니다. 이 경우에 모델의 성능이 급격하게 안좋아집니다.
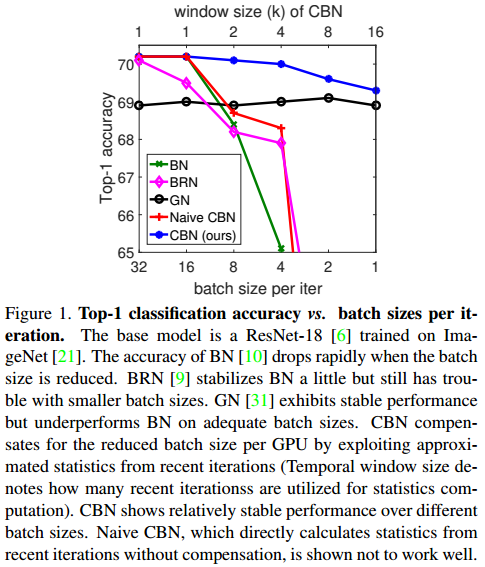
위 그림을 살펴보면 batch-size가 4,2,1 인 경우에 모델의 정확도가 급격하게 악화됩니다.
위 그림에 등장한 RBN, GN, Naive CBN에 대해 간단히 살펴보겠습니다.
GN은 channel dimension을 따라 다수의 그룹으로 feature map을 분할한 뒤에 각 그릅에서 평균과 분산을 계산하는 방법입니다. 이 방법은 작은 batch-size에도 준수한 효과를 나타냅니다. GN의 단점은 inference 속도를 느려지게 합니다. 따라서 real-time task에는 적합하지 않습니다.
RBN, Naive CBN은 iteration을 기준으로 평균과 분산을 계산하는 것입니다. 이 방법은 이전 iteration과 현재 iteration 간의 가중치 변화량을 전혀 고려하지 않고 계산합니다. 매 반복마다 가중치가 변화하므로, 현재 가중치에 해당하는 평균과 분산을 추정할 수 없습니다. 따라서 큰 K 를 사용하면 현재 가중치와 이전 k-1 가중치 사이에는 큰 차이가 존재하여 성능을 악화시킵니다. K는 평균과 분산을 계산하기 위해 얼마나 많은 반복을 활용할 것인지에 대한 값입니다.
Cross-Iteration Batch Normalization
본 논문에서 제안하는 CBN은 이전 반복에서 사용한 sample로 평균과 분산을 추정합니다. 매 반복마다 가중치가 갱신되므로 반복이 진행될수록 갱신된 만큼의 차이가 발생하게 됩니다. 따라서 이전 반복에서 사용한 sample로 평균과 분산을 계산하게 되면 현재 가중치에 해당하는 추정값과 차이가 발생합니다. 이는 오히려 성능에 악영향을 주어, 테일러 시리즈를 활용해 이전 가중치와 현재 가중치 차이를 compensation하여 근사화합니다.
CBN은 이전 가중치로 계산한 평균과 분산을 다음과 같이 compensation 합니다.

t-$\tau$ 번째 가중치로 계산한 평균과 분산을 테일러 시리즈로 compensation하여 현재 가중치로 계산한 평균과 분산으로 근사화 하는 것입니다. v는 E(x^2)를 의미합니다. v와 u를 안다면 v-u^2로 분산을 계산할 수 있습니다.
위 식이 성립할 수 있는 이유는, 매 반복마다 아주 작은 양의 가중치가 갱신된다는 가정을 하기 때문입니다. 이전과 현재의 가중치 차이가 적기 때문에 O()에 해당하는 고차항 테일러 시리즈는 생략되고 2차 테일러 시리즈만 남게 됩니다.
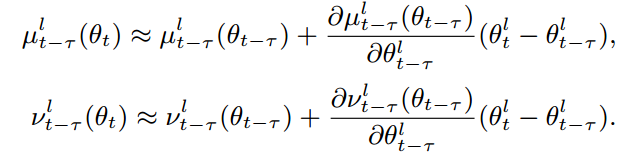

평균과 분산을 추정했으므로 x값에 normalization을 수행할 수 있습니다. k-1 번째까지 반복된 값을 활용하며 이를 평균하여 사용합니다.


v는 E(x^2)를 의미합니다. 이 논문에서 v 계산식에 max 연산을 사용합니다. 분산을 계산할 때 E(x^2)가 E(x)^2보다 커야 E(x^2) - E(x)^2을 만족합니다. v와 u는 테일러 시리즈로 근사화된 값이므로 E(x^2) > E(x)^2 조건을 위반할 수 있습니다. 따라서 max 연산을 사용합니다.
아래 그림은 compensation 유무에 따른 성능 비교입니다.
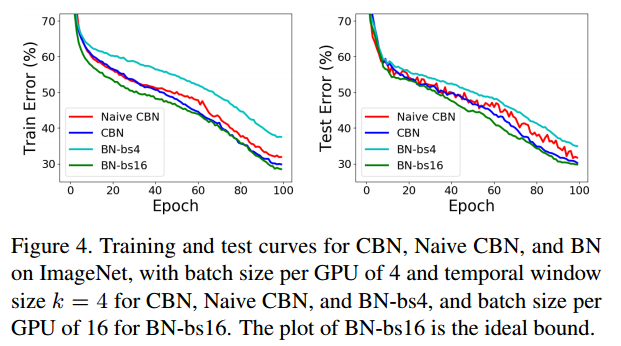
CBN의 하이퍼파라미터
CBN에서 몇 번째 반복을 사용할 것인지에 대한 k값을 하이퍼 파라미터로 사용합니다. 본 논문에서는 k를 window-size라고 표현하며 아래 식으로 k를 계산합니다.
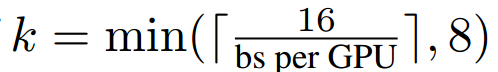
학습 초반에는 가중치가 급격하게 변하므로 k=1을 사용하라고 권합니다. CBN에서 k=1이 되면 일반적인 BN 연산을 수행합니다. k=1을 사용하는 기간을 burn-in period라고 표현하며 ImageNet classfication 에서는 25 epochs, COCO object detection에서는 3 epoch동안 burn-in period를 사용하라고 권합니다.
k값에 따른 성능 변화 입니다.
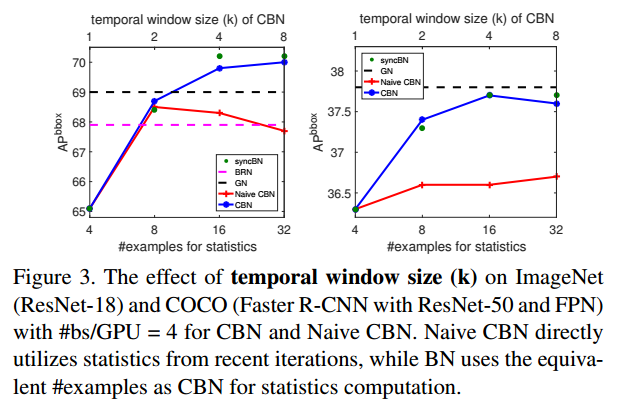
Performance


참고자료
[1] https://arxiv.org/abs/2002.05712
[2] https://www.youtube.com/watch?v=uiMQ3Fwal28
'논문 읽기 > Normalization' 카테고리의 다른 글
| [논문 읽기] Group Normalization(2018) (2) | 2021.07.04 |
|---|---|
| [논문 리뷰] 배치 정규화, Batch Normalization(2015) (2) | 2021.01.25 |