이번에 읽어볼 논문은 WRN, Wide Residual Networks 입니다.
WRN은 residual netowrk의 넓이를 증가시키고 깊이를 감소시킨 모델입니다. 16 layer로 이루어진 WRN은 1000-layer ResNet 같은 깊은 신경망을 제치고 SOTA를 달성했습니다. 신경망의 넓이를 증가한다는 의미는 filter수를 증가시킨다는 것을 의미합니다. 즉, WRN은 residual block을 구성하는 convolution layer의 filter 수를 증가시켜서 신경망의 넓이를 증가시켰습니다.
등장 배경
지금까지, CNN은 깊이를 증가시키는 방향으로 발전해왔습니다. 예를 들어, AlexNet, VGG, Inception, ResNet과 같은 모델이 있습니다. 모델의 깊이가 깊어지는 만큼 기울기 소실(gradient descent), 기울기 폭발(gradien explosion)과 같은 문제가 발생했습니다. 이 문제를 해결하기 위해 ResNet은 residual block 개념을 제안하였고, 이는 뛰어난 성능을 얻었습니다. 그리고, Residual block 내의 활성화 함수의 순서(Conv -BN -ReLU -> BN-ReLU-Conv)를 바꿔서 초기 입력값이 최종 출력값에 도달하도록 하는 Pre-Activation ResNet 을 제안하여 성능을 더 개선할 수 있었습니다.
이제 저자는 깊이와 활성화 함수의 순서를 제외하고, ResNet의 넓이에 따른 정확도 양상을 실험합니다. 그렇게 WRN은 탄생하게 되었습니다. 이 논문에서 Residual block의 넓이를 증가시키는 것이 모델의 깊이를 증가시키는 것보다 효과적으로 성능을 향상시킬 수 있다고 합니다. 그리고, 16-layer의 WRN은 1000-layer의 ResNet의 성능을 뛰어 넘는 결과를 보여줍니다. 심지어 학습 속도도 몇배는 빨랐습니다. 이를 통해 ResNet의 주 요인은 residual block이고, 깊이를 깊게하는 효과는 부수적이라고 합니다.
ResNet의 문제점
(1) circuit complexity theory
circuit complexity theory literature은 얇은 circuit는 깊은 circuit보다 더 많은 요소들을 필요로 한다는 이론입니다. 이를 신경망에 접목하여 생각해보면 깊은 신경망이 갖는 표현력을 얇은 신경망이 갖기 위해서는 엄청나게 넓은 신경망을 구성해야 된다고 생각해볼 수 있습니다. 그만큼 parameter 수도 증가하게 됩니다.
ResNet저자는 이 이론을 ResNet에 접목시켜 bottleneck 구조를 제안합니다. 이 구조는 모델을 얇게 해 parameter 수를 감소시켜 깊이를 증가시킵니다. residual block을 최대한 얇게 구성하여 모델의 깊이를 엄청나게 증가시켰습니다.
(2) Diminishing feature reuse
Diminishing feature reuse는 순전파에서 발생하는 문제로서, 기울기 소실과 비슷한 문제입니다. 입력과 가까운 계층이 학습한 특징이 최종 계층까지 도달하지 못하고 사라지는 문제입니다. 많은 수의 가중치가 곱해셔 발생합니다.
Diminishign feature reuse 문제를 해결하기 위해서 Stochastic Depth ResNet 논문에서 무작위로 residual block을 제거합니다. 하지만 이것은 dropout의 일종으로 생각해 볼 수 있습니다. 그래서 WRN은 diminishig feature reuse 문제를 다루기 위해 residual block에 dropout을 적용합니다. residual block 내에서 dropout은 convolutional layer 사이에 적용합니다.
즉, WRN은 (1) 문제를 넓이를 증가시켜서 해결하려 하고, (2) 문제는 residual block 내에있는 conv layer 사이에 dropout을 적용하여 해결하려 합니다.
WRN(Wide residual networks)
(1) Residual Block
ResNet은 두 종류의 residual block으로 구성됩니다.
- basic : 3x3conv - BN - ReLU - 3x3conv - BN - ReLU로 이루어져 있습니다. 아래 그림에서 (a)에 해당합니다.
- bottlenet : 1x1conv(차원 축소) - BN - ReLU - 3x3conv - BN - ReLU - 1x1conv(차원 확대) - BN - ReLU로 이루어져 있습니다. 아래 그림에서 (b)에 해당합니다. 이 구조는 모델을 얇게 만들기 위해 사용하므로 WRN에서는 사용하지 않습니다.
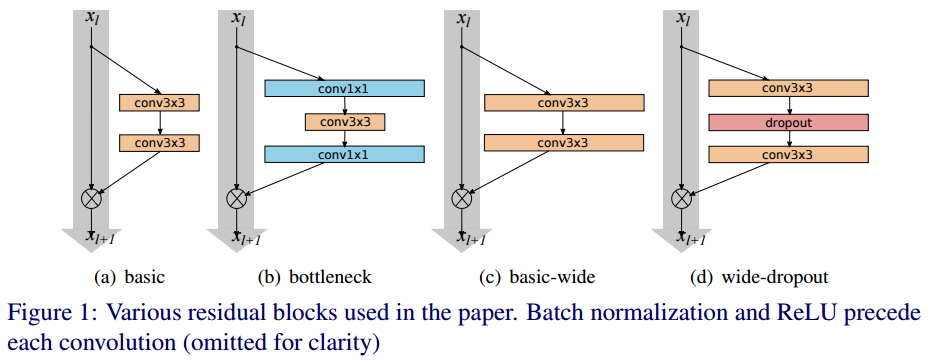
(c)와 (d)는 WRN의 residual block입니다. Pre-activation resnet 논문에서 제안된 활성화함수의 순서(BN - ReLU - conv)를 사용합니다. 그리고 각 conv layer가 갖고 있는 필터 수를 k배합니다. (d)는 conv와 conv 사이에 dropout을 적용한 것입니다.
(2) WRN archtecture
WRN의 구조는 다음과 같습니다.

conv1 이후에 3개의 residual block으로 구성되어 있습니다. B(3,3)은 conv layer의 kernel_size를 의미하고, 기존 conv layer의 필터수에 k배를 해줍니다. N이 WRN의 깊이를 결정합니다. N은 몇 개의 residual block이 묶여있는지를 의미합니다.
Experimental results
(1) Type of convolutions in a block
residual blcok을 구성하는 conv layer 개수와 kernel_size에 따른 성능 실험입니다. 예를 들어, B(1,3,1)은 1x1conv, 3x3conv, 1x1conv로 이루어진 residual block입니다.

(2) Number of convolutional layers per residual block
residual block을 구성하는 conv layer의 수에 따른 성능 실험입니다. l은 layer 수를 의미합니다.

(3) Width of residual blocks
깊이와 k에 따른 성능 실험입니다. k가 넓이를 결정하는 인자입니다. 넓이와 깊이의 비율을 잘 설정해야 좋은 성능을 얻습니다.

(4) Dropout in residual blocks
residual block내에 있는 conv layer 사이에 dropout을 적용했을 때와 안했을 때의 성능 비교입니다.

dropout을 적용하여 수렴 속도도 향상시킬 수 있었습니다.

Result
ImageNet dataset으로 학습된 ResNet와 WRN의 정확도를 비교한 표입니다.
WRN-50-2에서 50은 깊이, 2는 넓이 인자 k를 의미합니다.

참고자료
[1] www.bmva.org/bmvc/2016/papers/paper087/paper087.pdf
[2] towardsdatascience.com/review-wrns-wide-residual-networks-image-classification-d3feb3fb2004