이번에 소개할 논문은 Pre-Activation ResNet, Identity Mappings in Deep Residual Networks 입니다.
ResNet은 skip connection을 활용해 신경망이 수렴이 잘 되도록 하여 층을 깊게 쌓아 정확도를 높인 모델입니다. Pre-Activation ResNet은 기존의 residual block 구조에 활성화 함수의 순서를 바꿔 성능을 끌어올렸습니다. 입력값을 BN과 활성화 함수를 거친 뒤에 convolution layer에 전달한 것입니다. 아래 그림에서 기존 residual block과 pre-activation residual block을 확인할 수 있습니다.
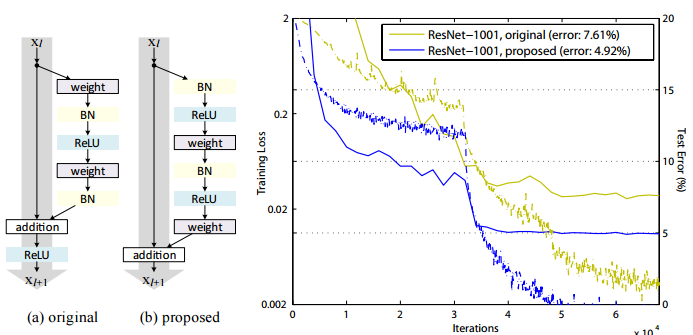
학습곡선에서 점선은 training loss, 굵은 선은 test error 입니다. proposed 구조의 test error, training loss가 original보다 낮습니다. 아래 표는 당시 state-of-the-art 기법들과의 비교입니다.

어떻게 순서를 바꿨고, 왜 성능이 향상되었는지 알아보겠습니다.
The Importance of Identity Mapping
우선 identity mapping의 중요성에 대해 설명합니다. 기존 residual block을 먼저 살펴보겠습니다.
ResNet은 이전 계층의 입력값 x를 identity mapping을 하여 출력값에 더해줍니다. 입력값 x를 identity mapping으로 감싸서 정보가 손실되지 않게 출력값으로 전달하는 것이 중요합니다. 그래야지 기울기 소실 문제가 발생하지 않기 때문입니다.
기존 ResNet의 Residual Unit 계산 식입니다.

h는 identity mapping, F는 residual function(convolution layer를 거칩니다.), xl은 입력값, xl+1은 출력값, f는 활성화 함수, W는 가중치를 의미합니다.
xl 입력값은 2~3개 convlayer를 거쳐서 F(xl, wl)이 되고, h(xl)과 더해져 yl을 생성합니다. 그리고 yl이 활성화 함수(ReLu)를 거쳐서 출력값 xl+1이 생성됩니다.
만약 f가 ReLU가 아니라 identity function이면 어떻게 될까요??
xl+1 = yl이 됩니다. 그러면 수식을 다음과 같이 쓸 수 있습니다.
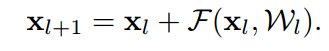
한번의 Residual block을 거치면 위 수식이 계산되어 xl+1이 생성되는 것입니다.
한번 더 Residual block 거치면 수식이 아래와 같이 됩니다.

여러 Residual block을 거친다면 위 식은 일반화 되어 다음과 같이 표현할 수 있습니다.
L은 최종 레이어를 의미합니다.

초기 입력값 xl이 최종 레이어 L까지 남아있게 됩니다. 이 xl은 역전파를 계산할 때 연쇄법칙을 거쳐서 1이 됩니다. 이 1이 남아있게 되어서 기울기 값이 소실되지 않게 되는 것입니다.

1이 남게 되어 역전파시에 신호를 끝까지 전달할 수 있습니다.
즉, f가 identity mapping이 된다면 순전파와 역전파시에 신호가 보존되어 기울기가 소실되지 않게 됩니다.
Pre-Activation
그러면 어떻게 f를 identity mapping으로 만들수 있을까요??
기존 ResNet에서는 f를 ReLU 함수와 BN을 사용합니다. 이 활성화 함수(ReLU와 BN)의 위치를 바꿔준다면 f를 identity mapping으로 만들 수 있습니다.
기존 ResNet 구조를 좀 더 살펴보겠습니다.
yl은 f 활성화 함수를 거쳐서 f(yl)이 됩니다.
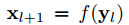
f(yl)은 residual block과 identity mapping 두 경로로 나뉘어 집니다. residual block을 거쳐 F(f(yl)+1,W)이 되고, identity mapping을 거쳐서 f(yl)이 됩니다. 이처럼 yl은 두 경로에 영향을 줍니다.

만약 f함수가 identity mapping 역할을 수행한다면 yl은 residual block 경로에만 영향을 미치게 됩니다.

이 f 함수는 addition 이후에 적용되는 활성화함수 ReLU 입니다. 이 f의 위치를 바꿔준다면 identity mapping 역할을 하도록 만들 수 있습니다. 아래 그림처럼 활성화 함수의 위치를 바꿔주면 addition에 아무것도 적용되지 않게 됩니다. 따라서 identity mapping이 됩니다.
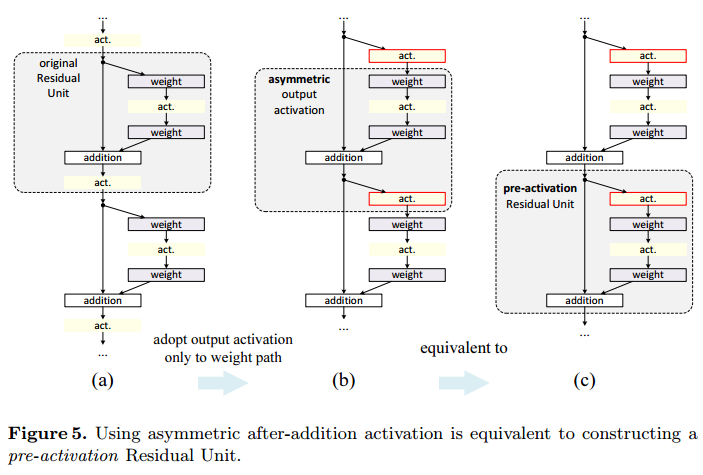
여기에 추가적으로 BN까지 적용하면 아래 그림과 같은 구조가 됩니다.
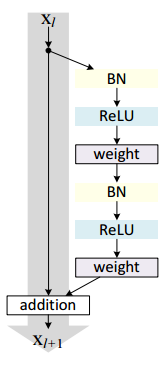
Residual block의 구조를 위 그림과 같이 변경하여 성능 향상이 이루어진 것입니다. 그림만 보더라도 회색 화살표에 있는 xl은 덧셈 이외에 아무런 연산이 적용되지 않습니다. 따라서 identity mapping이 된다고 생각해볼 수 있습니다.
Advantages of Pre-activation
Pre-activation의 장점은 두 가지 입니다.
1. Ease of Optimization
최적화를 쉽게 합니다. 이 효과는 깊은 신경망(1001-layer ResNet)을 학습시킬 때 분명하게 나타납니다. 기존 ResNet은 Skip connetion을 거쳐서 입력값과 출력값이 더해지고, ReLU 함수를 거칩니다. 더해진 값이 음수이면 ReLU 함수를 거쳐서 0이 됩니다. 만약, 층이 깊다면 이 증상의 영향이 더 커지게 되어 더 많은 값이 0이 될것입니다. 이때문에 초기 학습시에 불안정해져 수렴이 되지 않습니다. 실제로 학습 곡선을 보면 초기에 loss가 수렴되지 않는 모습을 볼 수 있습니다.
하지만 pre-activation 구조는 더해진 값이 ReLU 함수를 거치지 않아, 음수 값도 그대로 이용하게 됩니다. 실제로 학습 곡선을 살펴보면 제안된 구조가 초기 학습시에 loss를 더 빠르게 감소시킵니다.
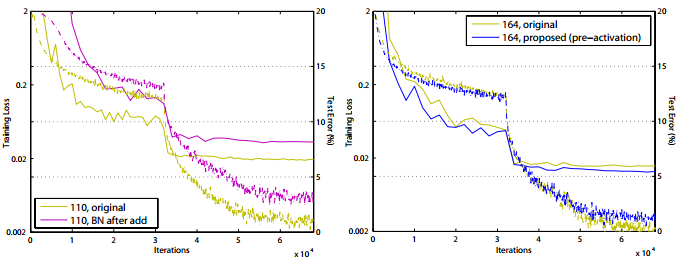
2. Reducing overfitting
위 그림을 보면 수렴지점에서 pre-activation 구조의 training loss가 original보다 높습니다. 반면에 test error가 낮은 것은 overfitting을 방지하는 효과가 있다는 것을 의미합니다.
논문에서 이 효과는 BN의 정규화 효과 때문에 발생한다고 추측합니다.

original Residual unit은 BN을 거치고 값이 short cut에 더해집니다. 따라서 더해진 값은 정규화되지 않습니다. 이 정규화되지 않은 값이 다음 convolution layer 입력값으로 전달됩니다.
Pre-activation Residual unit은 더해진 값이 BN을 거쳐서 정규화 된 뒤에 convolution layer에 입력됩니다. 따라서 overfitting을 방지한다고 저자는 추측합니다.
'논문 읽기 > Classification' 카테고리의 다른 글
| [논문 읽기] WRN(2016) 리뷰, Wide Residual Networks (0) | 2021.03.14 |
|---|---|
| [논문 읽기] Inception-v3(2015) 리뷰, Rethinking the Inception Architecture for Computer Vision (1) | 2021.03.13 |
| [논문 읽기] ResNet(2015) 리뷰 (2) | 2021.02.26 |
| [논문 리뷰] VGGNet(2014) 리뷰와 파이토치 구현 (4) | 2020.12.31 |
| [논문 리뷰] GoogLeNet (2014) 리뷰와 파이토치 구현 (3) | 2020.12.27 |