안녕하세요, 오늘 읽은 논문은 Dimensionality Reduction by Learning an Invariant Mapping 입니다. 해당 논문에서는 최초로 Contrastive Loss를 제안합니다.
Contrastive Loss는 차원 축소를 수행하는 함수를 만들기 위해 제안되었습니다. 차원 축소는 고차원의 입력 데이터를 저차원의 매니폴드로 map하는 것입니다. 동일한 종류의 입력 데이터를 차원 축소하면 이 둘은 매니폴드 상에 근처의 점으로 map 됩니다. 기존의 차원 축소 방법(PCA, LLE)들은 새로운 데이터가 입력되면 차원 축소를 위해 전체 데이터셋에 대해 계산을 해야합니다. 또한 function이 아닙니다.
논문에서는 training sample사이에 이웃 관계를 활용하여 저차원 매니폴드 공간으로 map하는 함수를 만듭니다. 근접 관계는 prior knowledge 또는 maual labeling, any distance metric으로부터 추출할 수 있습니다. 이 함수는 lightning change 및 geometric distortion 같은 입력값의 non-linear transformation 에 불변합니다. 또한 output space에 일관성을 갖고 smooth한 mapping을 합니다.
즉, 이 함수는 traning 동안 보지 못했던 data에 일관성있는 mapping을 하고, input space에서 distance measure에 제한되지 않습니다.
Learning the Low Dimensional Mapping
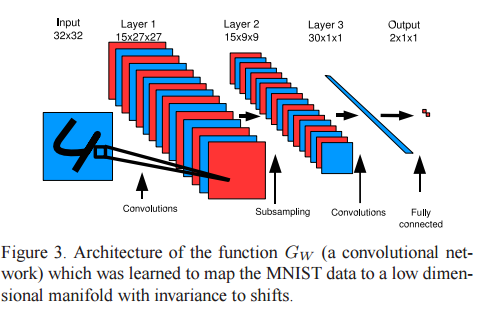
고차원의 패턴을 입력받아 저차원 출력값을 계산하는 함수를 만듭니다. 함수는 CNN입니다. 입력값 X가 CNN 함수 G를 거쳐서 저차원으로 mapping 합니다.
(1) Contrastive Loss Function
차원축소 함수를 만들기위해서 새로운 손실 함수인 Contrastive Loss Function을 제안합니다.
두개의 이미지에 0과 1 이진 label을 사용하여 CNN에 입력합니다. 두 데이터가 동일한 class이면 0, 서로 다른 class이면 1입니다. 두 이미지를 CNN에 통과하여 결과값을 출력합니다. 논문에서는 MNIST dataset을 사용하는데, 각 샘플에 가장 가까운 거리에 있는 data 5개를 pair(Y=0) 합니다. 그리고 나머지 pair는 dispair(Y=1) 합니다.
두 data는 파라미터를 공유하는 두 개의 CNN에 전달하여 G(x1), G(x2)를 출력합니다. 그리고 G(x1), G(x2) 사이에 L2 Norm을 계산하여 loss function에 활용합니다.


위 식에서 Ls는 similar pair사이의 loss, Ld는 dispair 사이의 loss 입니다. Ls와 Ld를 풀어쓰면 아래와 같이 됩니다.

m은 margin이며 G(X)의 반지름을 결정합니다. 이 반지름 내에있는 dispair만 loss에 기여합니다. 이렇게 Ld를 설정하면, Dw는 m과 동일할 시에 loss가 0이 됩니다. 즉, dispair가 입력된 경우에 Dw가 m과 동일하도록 합니다. 이 말은 두 쌍의 dispair이 거리 m을 갖도록 밀어내는 것을 의미합니다. 반면에 pair가 입력되면 Y=0이 되어 첫 번째 항만 존재하게 되는데 이는 두 pair가 항상 가까워지도록 합니다. margin을 설정한 이유는, margin 없이 loss를 최소화하는 경우에 신경망의 파라미터가 L=0이 되도록 상수가 될 수 있다고 합니다.


작동 방식

Performance
실험은 MNIST dataset에서 4와 9만을 이용합니다. 이 둘을 아래처럼 clustering 수행합니다.

입력 이미지가 translate 된 경우에도 clustering을 잘 수행합니다.

3D image에서도 잘 수행합니다. 이미지의 lightness에 불변하게 clustering을 수행합니다.

참고자료
[1] http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf