https://www.edwith.org/bayesiandeeplearning/joinLectures/14426
Bayesian Deep Learning 강좌소개 : edwith
- 최성준
www.edwith.org
최성준 교수님의 Bayesian Deep Learning 강의를 정리합니다.
측도론(Measure Theory)
주어진 Universal set U에 대하여 measuer은 U의 각 subset에 nonnegative real number를 할당합니다.
Set function
- set의 숫자를 할당하는 함수(Cardinality, length, area)
$\sigma$-field $\beta$
- 면적을 주기 위해 필요한 최소 단위
- sigma field 내에 존재하는 부분 집합은 measure을 부여할 수 있는 최소 단위
- set이 있을 때 가장 잘게 나눌 수 있는 조건이 모든 가능한 subset을 모운 power set인데 이를 $\sigma$-field $\beta$로 이해
- 아래의 조건을 만족하는 부분 집합

Properties of $\sigma$-field $\beta$
- $\sigma$-field 는 measure를 정의하기 위해 설계되었다.
- 확률이 measure.
- 어떤 요소가 시그마 필드에 존재하지 않는다면 measure가 될 수 없다.

measurable space
- 시그마 필드에 존재하지 않는 요소는 measure을 정의할 수 없다. 이 의미는 확률, 무게 등 정의를 못한다. 따라서 universal set U와 U의 부분 집합의 시그마 필드는 measurable space를 형성한다.
measure
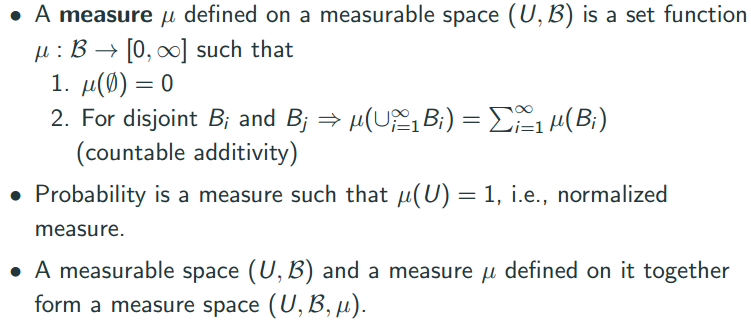
'수학 > Bayesian' 카테고리의 다른 글
| [Bayesian] 랜덤 프로세스(Random Process) (0) | 2021.07.28 |
|---|---|
| [Bayesian] 집합론(Set Theory) (0) | 2021.07.25 |