딥러닝 공부방

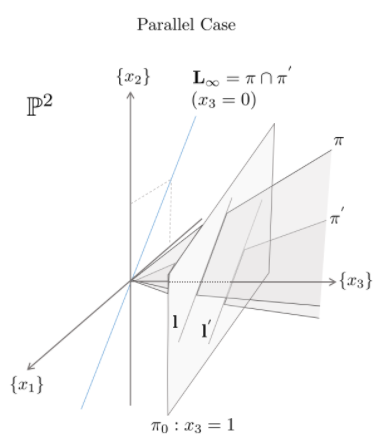
평행한 선의 교점(Intersection of parallel lines) 두 평행한 직선은 유클리드 공간에서는 만나지 않지만, 사영 공간 $P^2$에서는 만납니다. 두 선 ax + by + c = 0과 ax + by + c' = 0을 고려하겠습니다. 이 둘은 l = (a, b, c)^T 와 l' = (a, b, c')^T로 나타낼 수 있습니다. 이 둘의 교점을 구하는 것은 어렵지 않습니다. 이전 포스팅에서 배웠던 것 처럼 두 선을 외적하면 됩니다. 여기서 scale factor (c' - c)를 무시하면, 아래와 같은 교점이 됩니다. 이 점을 inhomogeneous로 표현하면, 아래와 같습니다. 이는 2 차원 euclidean 공간에서 유한한 점에 해당하지 않습니다. 이를 homogeneous coo..

선의 동치 표현(Homogeneous representation of lines) 평면에 존재하는 선은 ax + by + c = 0 과 같은 방정식으로 표현될 수 있습니다. 이를 직선의 방정식이라고 하는데, 어떤 a,b,c를 선택하느냐에 따라 다른 선이 됩니다. 따라서, 선은 일방적으로 벡터 (a,b,c)^T로 표현합니다. 이는 열벡터를 의미합니다. 선과 벡터 (a,b,c)^T는 one-to-one 대응이 아닙니다. 동치 좌표(homogeneous coordinates)에 의해서 선 ax + by + c = 0은 선 (ka)x + (kb)y + (kc) = 0와 동일합니다. 따라서, 벡터 (a,b,c)^T와 k(a,b,c)^T는 동일한 선을 나타냅니다. 그리고 이러한 관계에 있는 벡터들을 동치류(equi..