평행한 선의 교점(Intersection of parallel lines)
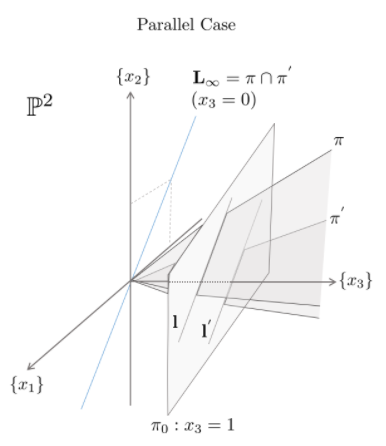
두 평행한 직선은 유클리드 공간에서는 만나지 않지만, 사영 공간 $P^2$에서는 만납니다.
두 선 ax + by + c = 0과 ax + by + c' = 0을 고려하겠습니다. 이 둘은 l = (a, b, c)^T 와 l' = (a, b, c')^T로 나타낼 수 있습니다. 이 둘의 교점을 구하는 것은 어렵지 않습니다. 이전 포스팅에서 배웠던 것 처럼 두 선을 외적하면 됩니다.
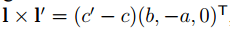
여기서 scale factor (c' - c)를 무시하면, 아래와 같은 교점이 됩니다.

이 점을 inhomogeneous로 표현하면, 아래와 같습니다.

이는 2 차원 euclidean 공간에서 유한한 점에 해당하지 않습니다. 이를 homogeneous coordinate (x, y, 0)^T로 표현하여 2차원 projective 공간의 점에 해당합니다. 이를 평행한 선은 무한에서 만난다고 여깁니다.
예제 문제를 풀어보겠습니다. 두 직선 x=1, x=2가 존재하는 경우에 두 직선은 평행하며 무한에서 교차합니다. homogeneous 표현으로 다음과 같이 나타낼 수 있습니다.


이 두선을 외적하면 두 선에 교차하는 점을 찾을 수 있습니다.
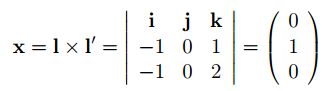
이에 해당하는 점은 y축 방향으로 무한대 점(point at infinity)입니다.
이상점과 무한대 선(Ideal points and the line at infinity)
Homogeneous vectors x = (x1, x2, x3)^T는 R2 공간에서 유한 점에 해당합니다. x3=0이라면, 모든 homogeneous 3-vector의 집합입니다. 이는 사영 공간(Projective space) P^2에 해당합니다. 마지막 좌표가 x3=0인 경우에, 이상점(ideal points) 또는 무한대 점(points at infinity)라고 부릅니다. 모든 이상점의 집합은 (x1, x2, 0)^T로 표현합니다.
이상점의 집합은 하나의 직선에 놓여있습니다. 이 직선은 무한대 선(line at infinity)이며, 다음과 같이 표기합니다.

이상점은 무한대 선에 놓여있으므로 둘의 내적 또는 둘 중 하나를 전치한 것의 곱은 0이 됩니다.

이전 포스팅에서 직선 l = (a,b,c)^T는 무한대의 선과 이상점(b,-a,0)^T에서 교차한다는 것을 배웠습니다. 이상점은 모든 선에 놓여있기 때문입니다.

선 l' = (a, b, c')^T는 선 l에 평행하고, c'와 관계 없이 무한대의 선의 이상점(b,-a,0)^T에서 교차합니다. inhomogeneous 표기법으로 (b,-a)^T는 선에 접하는 벡터이고, 노말 벡터(a,b)에 직교합니다. 따라서 inhomogeneous 표기 (b,-a)^T는 선의 방향을 나타냅니다. 무한대의 선은 평면에서 선들의 방향의 집합으로 생각할 수 있습니다.
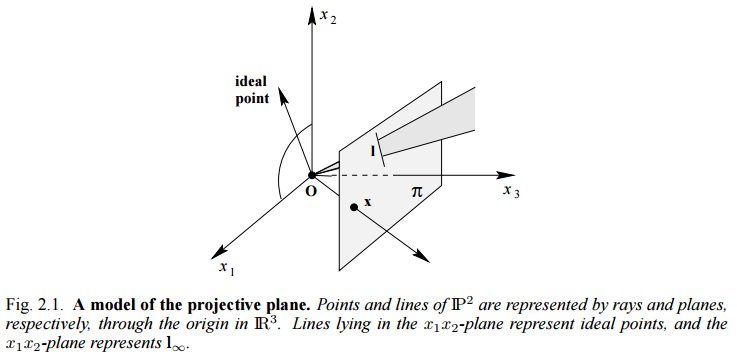
사영 공간 P^2에서 서로 다른 선은 하나의 점에서 만나고, 두 서로 다른 점은 하나의 선에 놓여있습니다. 이 사실은 Euclidean 기하학에서 평행한 직선인 경우에 성립하지 않습니다.
참고자료
[1] https://edward0im.github.io/mathematics/2020/06/03/multiple-view-geometry1/#org6300343
[2] Multiple View Geometry in Computer Vision