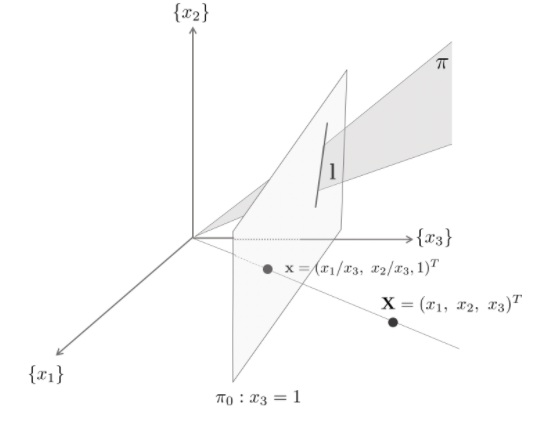
A model for the projective plane 사영 공간(projective space) P^2는 Euclidean 공간 R^3에서 원점을 지나는 모든 직선의 집합으로 생각할 수 있습니다. k에 따라 변화하는 모든 벡터 k(x1,x2,x3)^T의 집합은 원점을 지나는 직선을 형성합니다. 이러한 직선은 사영 공간 P^2에서 한 점을 나타냅니다. 이러한 관점으로 P^2에서 선은 원점을 지나는 평면을 의미합니다. 두 직선은 한 평면에 놓여있고, 임의의 두 평면은 직선에서 교차합니다. P^2 공간에서는 스케일 값에 관계없이 한 점을 유일하게 정의할 수 있으므로 마지막 항 x3로 좌표값을 나눈 (x1/x3, x2/x3, 1)을 일반적으로 한 점을 표현하는 대표값으로 간주합니다. R^3 공간 상의 원점..