(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 작성하였습니다.
신경망 학습 (3) - 학습 알고리즘 구현
지금까지 배운 내용을 이용해서 신경망 학습 알고리즘을 구현해보겠습니다.
5. 학습 알고리즘 구현하기
신경망 학습의 절차는 다음과 같습니다.
전체
신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 '학습'이라 합니다. 신경망 학습은 다음과 같이 4단계로 수행합니다.
1단계 - 미니배치
훈련 데이터 중 일부를 무작위로 가져옵니다. 이렇게 선별한 데이터를 미니배치라 하며, 그 미니배치의 손실 함수 값을 줄이는 것이 목표입니다.
2단계 - 기울기 산출
미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구합니다. 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시합니다.
3단계 - 매개변수 갱신
경사하강법을 이용하여 가중치 매개변수를 기울기 방향으로 아주 조금 갱신합니다.
4단계 - 반복
1~3단계를 반복합니다.
위의 순서는 확률적 경사 하강법(SGD, stochastic gradient descent) 을 이용한 방법입니다. 데이터를 미니배치로 무작위로 선정하기 때문에 SGD라고 부릅니다. '확률적으로 무작위로 골라낸 데이터'에 대해 수행하는 경사 하강법이라는 의미입니다.
그럼 실제로 손글씨 숫자를 학습하는 신경망을 구현해보겠습니다. 여기에서는 2층 신경망을 대상으로 MNIST 데이터셋을 사용하여 학습을 수행합니다.
5.1 2층 신경망 클래스 구현하기
2층 신경망을 하나의 클래스로 구현
class TwoLayerNet:
# 초기화 수행 메서드
# params는 신경망의 매개변수를 보관하는 딕셔너리 변수(인스턴스 변수)
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {} # 가중치 초기화
self.params['W1'] = weight_init_std * \
np.random.randn(input_size, hidden_size) # (입력 X 은닉층) 행렬의 가중치 생성
self.params['b1'] = np.zeros(hidden_size) # 은닉층 노드수만큼 편향 생성, 0으로 설정
self.params['W2'] = weight_init_std * \
np.random.randn(input_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
# 예측(추론) 수행 메서드, x : 이미지 데이터
def predic(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.parmas['b2']
a1 = np.dot(x, W1) + b1 # 활성화 함수 입력 데이터
z1 = sigmoid(a1) # 활성화 함수 출력 ( 시그모이드 사용)
a2 = np.dot(z1, W2) + b2
y = softmax(a2) # 소프트맥스 함수는 확률로 해석가능 (총합이 1)
return y
# 손실 함수 값을 구하는 매서드 x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
# 정확도 측정하는 메서드
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1) # y행렬의 1차원 요소 최대값 추출
y = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 가중치 매개변수의 기울기를 구하는 메서드
# grads는 기울기 보관하는 딕셔너리 변수(numerical_gradient의 반환값)
def numerical_gradient(self, x, t)
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1']) # 편향도 갱신해줘야 한다.
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
# 오차역전파법을 사용하여 기울기를 효율적이고 빠르고 계산할 수 있습니다.
# def gradient(self, x, t) 오차역전파법은 다음 포스팅에서 공부하도록 하겠습니다.
오차역전파법
numerical_gradient(self, x, t)는 수치 미분 방식으로 매개변수의 기울기를 계산합니다. 오차 역전파법은 이 기울기 계산을 고속으로 수행하는 기법입니다. 수치 미분을 사용할 때와 거의 같은 결과를 훨씬 빠르게 얻을 수 있습니다.
5.2 미니배치 학습 구현하기
미니배치 학습이란 훈련 데이터 중 일부를 무작위로 꺼내고(미니배치), 그 미니배치에 대해서 경사법으로 매개변수를 갱신합니다.
미니배치 구현
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
train_loss_list = []
# 하이퍼파라미터(사용자가 지정해줘야하는 변수)
iters_num = 10000 # 반복 횟수
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.numerical_gradient(x_batch, t_batch)
# grad - network.gradient(x_batch, t_batch) 오차역전법을 통한 성능개선
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
코드 작동 순서
1. 60,000개의 훈련 데이터에서 임의로 100개의 데이터(이미지 데이터와 정답 레이블 데이터)를 추려냅니다.
2. 100개의 미니배치를 대상으로 확률적 경사 하강법을 수행해 매개변수를 갱신합니다.
3. 갱신 횟수(반복 횟수)를 10,000번으로 설정하고, 갱신할 때마다 훈련 데이터에 대한 손실 함수를 계산하고 그 값을 배열에 추가합니다.
이 손실 함수의 값이 변화하는 추이를 그래프로 확인해보겠습니다.
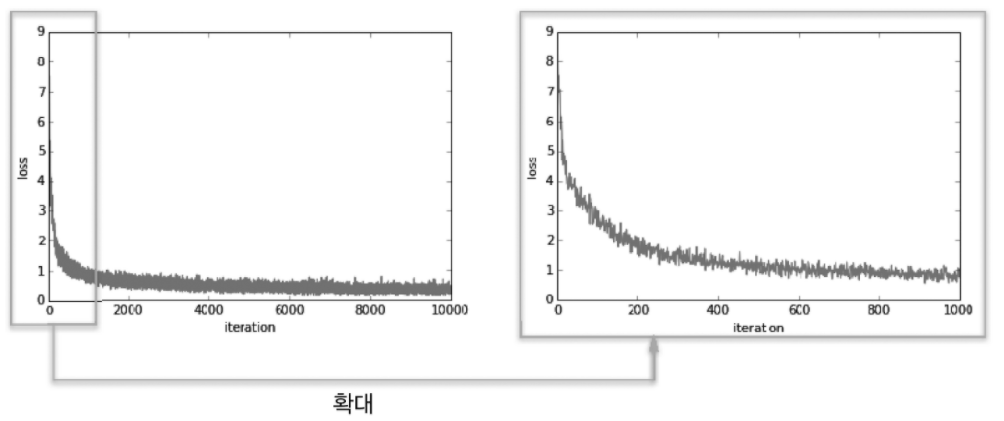
학습 횟수가 늘어가면서 손실 함수의 값이 줄어드는 것을 확인할 수 있습니다.
5.3 시험 데이터로 평가하기
신경망 학습에서는 훈련 데이터 외의 데이터를 올바르게 인식하는지를 확인해야 합니다. 위의 손실 함수의 값은 '훈련 데이터의 미니배치에 대한 손실 함수'의 값이기 때문입니다. 다른 말로 '오버피팅'을 일으키지 않는지 확인해야 합니다. 오버피팅되었다는 것은, 예를 들어 훈련 데이터에 포함된 이미지만 제대로 구분하고, 그렇지 않은 이미지는 식별할 수 없다는 뜻 입니다.
신경망 학습의 원래 목표는 범용적인 능력을 익히는 것입니다. 범용 능력을 평가하려면 훈련 데이터에 포함되지 않은 데이터를 사용해 평가해봐야합니다. 이를 위해 다음 구현에서는 학습 도중 정기적으로 훈련 데이터와 시험 데이터를 대상으로 정확도를 기록합니다.
1에폭(epoch)별로 훈련 데이터와 시험 데이터에 대한 정확도를 기록해봅시다.
에폭(epoch)은 하나의 단위입니다.
1에폭은 학습에서 훈련 데이터를 모두 소진했을 때의 횟수에 해당합니다. 예컨대 훈련 데이터 10,000개를 100개의 미니배치로 학습할 경우, 확률적 경사 하강법을 100회 반복하면 모든 훈련 데이터를 '소진'한 게 됩니다. 이 경우 100회가 1에폭이 됩니다.
1epoch당 정확도를 구현한 2층 신경망 구현 (시험 데이터로 평가하기 위해)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 하이퍼파라미터(사용자가 지정해줘야하는 변수)
iters_num = 10000 # 반복 횟수
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 1epoch당 반복 수
iter_per_epoch = max(train_size / batch_size, 1) # 훈련 데이터 수 / 미니 배치 수
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.numerical_gradient(x_batch, t_batch)
# grad - network.gradient(x_batch, t_batch) 오차역전법을 통한 성능개선
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1epoch당 정확도 계산
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print('train acc, test acc : ' + str(train_acc) + ', ' + str(test_acc))1애폭마다 모든 훈련 데이터와 시험 데이터에 대한 정확도를 계산하고, 그 결과를 가록합니다. 정확도를 1에폭마다 계산하는 이유는 for 문 안에서 매번 계산하기에는 시간이 오래 걸리고, 그렇게까지 자주 기록할 필요도 없기 때문입니다.
앞의 코드로 얻은 결과를 그래프로 그려보겠습니다.

에폭이 진행될수록(학습이 진행될수록) 훈련 데이터와 시험 데이터를 사용하고 평가한 정확도가 모두 좋아지고 있는 것을 확인할 수 있습니다. 이번 학습에서는 오버 피팅이 일어나지 않았습니다.
오버피팅이 일어났을 경우
훈련이란 훈련 데이터에 대한 정확도를 높이는 방향으로 학습하는 것이니 그 정확도는 에폭을 반복할 수록 높아집니다. 반면 훈련 데이터에 지나치게 적응하면, 즉 오버피팅되면 훈련 데이터와는 다른 데이터를 보면 잘못된 판단을 하기 시작합니다. 어느 순간부터 시험 데이터에 대한 정확도가 점차 떨어지기 시작합니다. 이 순간이 오버피팅이 시작되는 순간입니다.
조기 종료(early stopping)
시험 데이터에 대한 정확도가 떨어지기 시작하는 순간을 포착해 학습을 중단하면 오버피팅을 예방할 수 있습니다. 이 기법을 조기 종료(early stopping)이라고 합니다.
6. 정리
신경망 학습에 대해서 공부했습니다. 신경망 학습을 구현하기 위해 미니배치, 손실함수, 기울기, 경사법, 시험데이터로 평가를 공부했습니다. 다음에는 기울기를 효율적으로 계산하는 '오차역전파법'을 배워보도록 하겠습니다.
03. 신경망 학습 에서 배운 내용
1. 기계학습에서 사용하는 데이터셋은 훈련 데이터와 시험 데이터로 나눠 사용한다.
2. 훈련 데이터로 학습한 모델의 범용 능력을 시험 데이터로 평가한다.
3. 신경망 학습은 손실 함수를 지표로, 손실 함수의 값이 작아지는 방향으로 가중치 매개변수를 갱신한다.
4. 가중치 매개변수를 갱신할 때는 가중치 매개변수의 기울기를 이용하고, 기울어진 방향으로 가중치의 값을 갱신하는 작업을 반복한다.
5. 아주 작은 값을 주었을 때의 차분으로 미분하는 것을 수치 미분이라고 한다.
6. 수치 미분을 이용해 가중치 매개변수의 기울기를 구할 수 있다.
7. 수치 미분을 이용한 계산에는 시간이 걸리지만, 그 구현은 간단하다. 오차역전파법을 이용하면 기울기를 빠르게 구할 수 있다.
'수학 > 딥러닝 이론' 카테고리의 다른 글
| 04-2. 오차역전파법 (2) - 간단한 역전파 계층 구현 (0) | 2020.09.12 |
|---|---|
| 04-1. 오차역전파법 (1) - 계산 그래프와 연쇄법칙 (0) | 2020.09.11 |
| 03-2. 신경망 학습 (2) - 기울기와 경사하강법 (0) | 2020.09.11 |
| 03-1. 신경망 학습 (1) - 손실 함수와 수치 미분 (0) | 2020.09.10 |
| 02-2. 신경망 (2) - 출력층 설계와 MNIST 구현 (6) | 2020.09.09 |