(밑바닥부터 시작하는 딥러닝, 사이토고치) 를 바탕으로 작성하였습니다.
오차역전파법 (1) - 계산 그래프와 연쇄법칙
이전의 포스팅에서는 신경망 학습을 공부했습니다. 그때 신경망의 가중치 매개변수에 대한 손실 함수의 기울기는 수치 미분을 사용해 구했습니다. 수치 미분은 단순하고 구현하기도 쉽지만 계산 시간이 오래 걸린다는 게 단점입니다.
이번 포스팅에서는 가중치 매개변수의 기울기를 효율적으로 계산하는 '오차역전파법(backpropagation)'을 이해하기 위해 계산 그래프와 연쇄법칙에 대해 공부하겠습니다.
1. 계산 그래프 - Computational graph
계산 그래프(computational graph)는 계산 과정을 그래프로 나타낸 것입니다. 여기에서 그래프는 복수의 노드(node)와 에지(edge)로 표현됩니다. (노드 사이의 직선을 '에지'라고 합니다.)
이번 절에는 계산 그래프에 친숙해지기 위한 간단한 문제를 풀어보겠습니다. 간단한 문제에서부터 한 단계씩 나아가면서 마지막에는 오차역전파법에 도달할 예정입니다.
1.1 계산 그래프로 풀다.
간단한 문제를 계산 그래프를 사용해서 풀어보겠습니다.
문제 1 : 현빈 군은 슈퍼에서 1개에 100원인 사과를 2개 샀습니다. 이때 지불 금액을 구하세요. 단, 소비세가 10% 부과됩니다.
계산 그래프는 계산 과정을 노드와 화살표로 표현합니다. 노드는 원으로 표기하고 원 안에 연산 내용을 적습니다. 또, 각 노드의 계산 결과가 왼쪽에서 오른쪽으로 전해지게 합니다.

사과 100원이 'X2' 노드로 흐르고, 200원이 되어 다음 노드로 전달됩니다. 이제 200원이 'X1.1' 노드를 거쳐 220원이 됩니다.
다른 방법으로는 노드 안에 곱셈인 'X'만을 연산으로 생각할 수 있습니다. 이렇게 하면 '2'와 '1.1'은 각각 '사과의 개수'와 '소비세' 변수가 되어 원밖에 표기하게 됩니다.

그럼 다음 문제입니다.
문제 2 : 현빈 군은 슈퍼에서 사과를 2개, 귤을 3개 샀습니다. 사과는 1개에 100원, 귤은 1개 150원입니다. 소비세가 10%일 때 지불 금액을 구하세요

이 문제에는 덧셈 노드인 '+'가 새로 등장하여 사과와 귤의 금액을 합산합니다.
지금까지 살펴본 것처럼 계산 그래프를 이용한 문제풀이는 다음 흐름으로 진행합니다.
1. 계산 그래프를 구성한다
2. 그래프에서 계산을 왼쪽에서 오른쪽으로 진행한다.
계산 그래프에서 순전파(foward propagation)와 역전파(backword propagation)
순전파: '계산을 왼쪽에서 오른쪽으로 진행'하는 단계를 의미합니다. 순전파는 계산 그래프의 출발점부터 종착점으로의 전파입니다.
역전파: '오른쪽에서 왼쪽으로 진행'하는 것을 의미합니다. 역전파는 이후에 미분을 계산할 때 중요한 역할을 합니다.
1.2 국소적 계산
국소적 계산은 결국 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만으로 결과를 출력할 수 있는 것입니다. 계산 그래프의 특징은 '국소적 계산'을 전파함으로써 최종 결과를 얻는다는 점에 있습니다. 국소적이란 '자신과 직접 관계된 작은 범위'라는 뜻 입니다.
국소적 계산의 구체적인 예로 사과 2개를 포함한 여러 식품을 구입하는 경우를 생각해 보겠습니다.
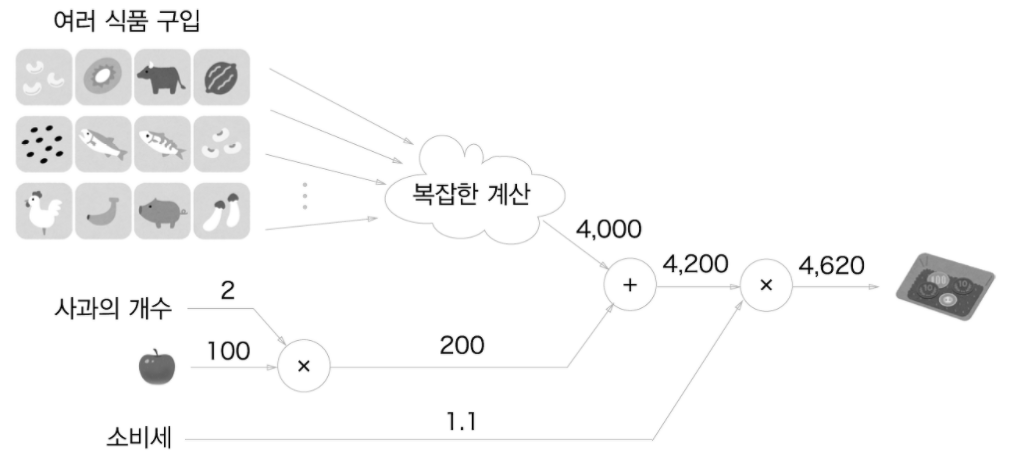
여기서 핵심은 각 노드에서의 계산은 국소적 계산이라는 점입니다. 사과와 그 외의 물품 값을 더하는 계산(4,000 + 200 -> 4,200)은 4,000이라는 숫자가 어떻게 계산되었느냐와는 상관없이, 단지 두 숫자를 더하면 된다는 의미입니다. 각 노드는 자신과 관련한 계산 외에는 아무것도 신경 쓸게 없습니다.
이처럼 계산 그래프는 국소적 계산에 집중합니다. 전체 계산이 제아무리 복잡하더라도 각 단계에서 하는 일은 해당 노드의 '국소적 계산'입니다. 국소적인 계산은 단순하지만, 그 결과를 전달함으로써 전체를 구성하는 복잡한 계산을 해낼 수 있습니다.
계산 그래프를 이용하면 전체를 구성하는 복잡한 계산을 해낼 수 있다!
1.3 왜 계산 그래프로 푸는가?
계산 그래프의 이점
1. 국소적 계산
전체가 아무리 복잡해도 각 노드에서는 단순한 계산에 집중하여 문제를 단순화 할 수 있습니다.
2. 중간 계산 결과를 모두 보관할 수 있습니다.
예를 들어 사과 2개까지 계산했을 때의 200원, 소비세를 더하기 전의 금액은 650원인 식으로 중간 결과를 보관합니다.
3. 역전파를 통해 '미분'을 효율적으로 계산할 수 있습니다.
역전파를 통해 사과 가격이 오르면 최종 금액에 어떤 영향을 미치는지 알 수 있습니다. 이는 '사과 가격에 대한 지불 금액의 미분'에 해당합니다. 기호로 나타낸다면 사과 값을 $x$, 지불 금액을 L이라 했을 때 $\frac{\partial L}{\partial x}$을 구하는 것 입니다. 이 미분 값은 사과 값이 '아주 조금' 올랐을 때 지불 금액이 얼마나 증가하느냐를 표시한 것입니다. 이를 역전파를 통해 구할 수 있습니다.
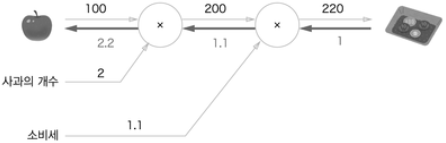
역전파는 '국소적 미분(편미분)'을 전달하고 오른쪽에서 왼쪽으로 '1 -> 1.1 -> 2.2' 순으로 미분 값을 전달합니다. 이 결과로부터 '사과 가격에 대한 지불 금액의 미분'값은 2.2라고 할 수 있습니다. 사과가 1원 오르면 최종 금액은 2.2원 오른다는 의미입니다.
'소비세에 대한 지불 금액의 미분'이나 '사과 개수에 대한 지불 금액의 미분'도 같은 순서로 구할 수 있습니다. 그리고 그 때는 중간까지 구한 미분 결과를 공유할 수 있어서 다수의 미분을 효율적으로 계산할 수 있습니다. 이처럼 계산 그래프의 이점은 순전파와 역전파를 활용해서 '각 변수의 미분을 효율적으로 구할 수 있다'는 것입니다.
2. 연쇄법칙 - Chain rule
'국소적 미분'을 전달하는 원리는 연쇄법칙(chain rule)에 따른 것입니다. 이번에는 연쇄법칙을 설명하고 그것이 계산 그래프 상의 역전파와 같다는 사실을 밝히겠습니다.
2.1 계산 그래프의 역전파
먼저, 예시로 $y$ = $f(x)$의 역전파를 살펴보겠습니다.
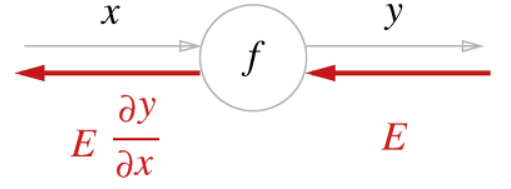
역전파의 계산 절차는 신호 E에 노드의 국소적 미분($\frac{\partial y}{\partial x}$)을 곱한 후 다음 노드로 전달합니다. 이러한 계산 순서를 따르면 목표로 하는 미분 값을 효율적으로 구현할 수 있다는 것이 역전파의 핵심입니다. 이유는 연쇄법칙의 원리로 설명할 수 있습니다.
1.2 연쇄법칙이란?
연쇄법칙을 설명하려면 우선 합성 함수 이야기부터 시작해야 합니다. 합성 함수란 여러 함수로 구성된 함수입니다. 예를 들어 $z$ = $(x + y)^2$라는 식은 다음의 식처럼 두 개의 식으로 구성됩니다.
$$z = t^2$$
$$t = x + y$$
연쇄법칙은 합성 함수의 미분에 대한 성질이며, 다음과 같이 정의됩니다.
합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
이것이 연쇄법칙의 원리입니다. $z$ = $(x + y)^2$를 예로 설명하면 다음 식으로 나타낼 수 있습니다.
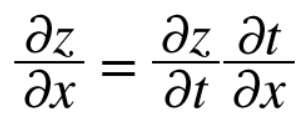
그럼 연쇄법칙을 써서 $\frac{\partial z}{\partial x}$를 구해봅시다.

그리고 최종적으로 구하고 싶은 $\frac{\partial z}{\partial x}$는 두 미분을 곱해 계산합니다.

2.3 연쇄법칙과 계산 그래프
연쇄법칙 계산을 계산 그래프로 나타내봅시다.
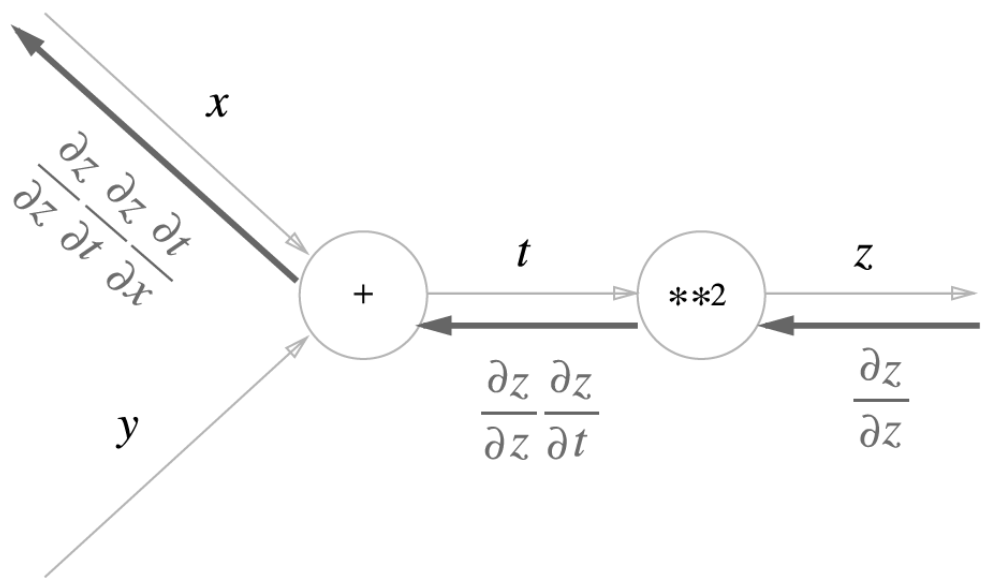
역전파의 계산 절차
노드로 들어온 입력 신호에 그 노드의 국소적 미분(편미분)을 곱한 후 다음 노드로 전달합니다.
위 그림에서 주목할 것은 맨 왼쪽 역전파입니다. $\partial z$와 $\partial t$는 전부 소거 되어 'x에 대한 z의 미분'이 됩니다. 즉, 역전파가 하는 일은 연쇄법칙의 원리와 같습니다.
위의 계산그래프에 $\frac{\partial z}{\partial t}$와 $\frac{\partial t}{\partial x}$의 결과를 대입하면 $\frac{\partial z}{\partial x}$는 2(x+y)임을 구할 수 있습니다.

이번 포스팅에서는 오차역전파법을 이해하기 위해 계산 그래프와 연쇄법칙을 알아보았습니다.
다음 포스팅에서는 역전파를 설명하고 사과 쇼핑 문제를 통해 간단한 역전파 계층을 구현하겠습니다. 감사합니다.
'수학 > 딥러닝 이론' 카테고리의 다른 글
| 04-3. 오차역전파법 (3) - 활성화 함수, Affine, Softmax 계층 구현 (1) | 2020.09.12 |
|---|---|
| 04-2. 오차역전파법 (2) - 간단한 역전파 계층 구현 (0) | 2020.09.12 |
| 03-3. 신경망 학습 (3) - 학습 알고리즘 구현 (1) | 2020.09.11 |
| 03-2. 신경망 학습 (2) - 기울기와 경사하강법 (0) | 2020.09.11 |
| 03-1. 신경망 학습 (1) - 손실 함수와 수치 미분 (0) | 2020.09.10 |