사이토고키의 <밑바닥부터 시작하는 딥러닝>을 공부하고 정리해보았습니다.
[딥러닝] 1. 가중치의 초깃값 - 초깃값을 0으로 하면?
사이토고키의 <밑바닥부터 시작하는 딥러닝>을 공부하고 정리해보았습니다. 가중치의 초깃값 신경망 학습에서 특히 중요한 것이 가중치의 초깃값입니다. 가중치의 초깃값을 무엇으로 설정��
deep-learning-study.tistory.com
이전 포스팅에서 가중치의 초깃값을 적절히 설정하면 각 층의 활성화값 분포가 적당히 퍼지면서 학습이 원활하게 수행됨을 배웠습니다.
배치 정규화 - Batch Normalization
그렇다면 각 층이 활성화를 적당히 퍼뜨리도록 '강제'해보자는 아이디어에서 출발할 것이 배치 정규화 방법입니다.
배치 정규화는 2015년에 제안된 방법입니다.
배치 정규화는 세상에 나온 지 얼마 안 된 기법임에도 많은 연구자와 기술자가 즐겨 사용하고 있습니다.
실제로 기계학습 콘테스트의 결과를 보면 이 배치 정규화를 사용하여 뛰어난 결과를 달성한 예가 많습니다.
배치 정규화가 주목받는 이유는 다음과 같습니다.
1. 학습을 빨리 진행할 수 있다(학습속도 개선).
2. 초깃값에 크게 의존하지 않는다(초깃값 선택 장애 개선)
3. 오버피팅을 억제한다(드롭아웃 등의 필요성 감소)
배치 정규화 알고리즘
배치 정규화의 기본 아이디어는 앞에서 말했듯이 각 층에서의 활성화 값이 적당히 분포되도록 조정하는 것입니다.
그래서 그림과 같이 데이터 분포를 정규화하는 '배치 정규화 계층'을 신경망에 삽입합니다.

배치 정규화는 그 이름과 같이 학습 시 미니배치를 단위로 정규화합니다.
구체적으로는 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화 합니다.
수식으로는 다음과 같습니다.

여기에는 미니배치 B = {$x_1, x_2, ... , x_m$}이라는 m개의 입력 데이터의 집합에 대해 평균 $\mu_b$와 분산 $\sigma_B^2$을 구합니다.
그리고 입력 데이터를 평균이 0, 분산이 1이 되게(적절한 분포가 되게) 정규화를 합니다.
그리고 $\epsilon$기호는 작은 값으로, 0으로 나누는 사태르 예방하는 역할입니다.
위 식은 단순히 미니배치 입력 데이터를 평균 0, 분산 1인 데이터로 변환(표준화)하는 일을 합니다.
이 처리를 활성화 함수의 앞에 삽입함으로써 데이터 부포가 덜 치우치게 할 수 있습니다.
또, 배치 정규화 계층마다 이 정규화된 데이터에 고유한 확대와 이동변환을 수행합니다.

이 식에서 $\gamma$가 확대를, $\beta$가 이동을 담당합니다.
두 값은 처음에는 $\gamma$ = 1, $\beta$ =0 부터 시작하고, 학습하면서 적합한 값으로 조정해갑니다.
이것이 배치 정규화의 알고리즘입니다.
이 알고리즘이 신경망에서 순전파 때 적용됩니다.
이를 계산 그래프로 다음과 같이 그릴 수 있습니다.
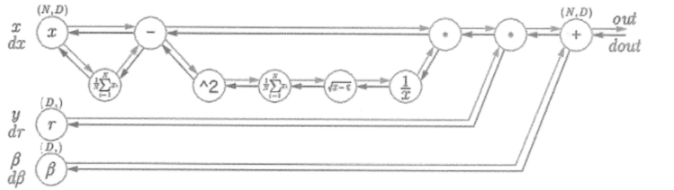
배치 정규화의 효과
배치 정규화 계층을 사용한 실험을 해보겠습니다.
우선은 MNIST 데이터셋을 사용하여 배치 정규화 계층을 사용할 떄와 사용하지 않을 떄의 학습 진도가 어떻게 달라지는지를 보겠습니다.
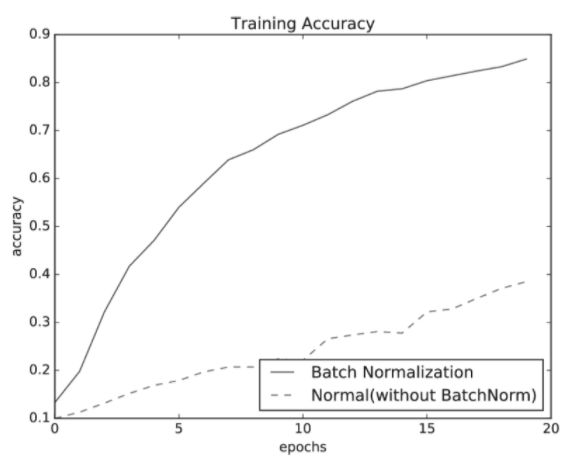
그림과 같이 배치 정규화가 학습을 빨리 진전시키고 있습니다.
계속해서 초깃값 분포를 다양하게 줘가며 학습 진행이 어떻게 달라지는지 보겠습니다.
아래 그림은 가중치 초깃값의 표준편차를 다양하게 바꿔가며 학습 경과를 관찰한 그래프입니다.
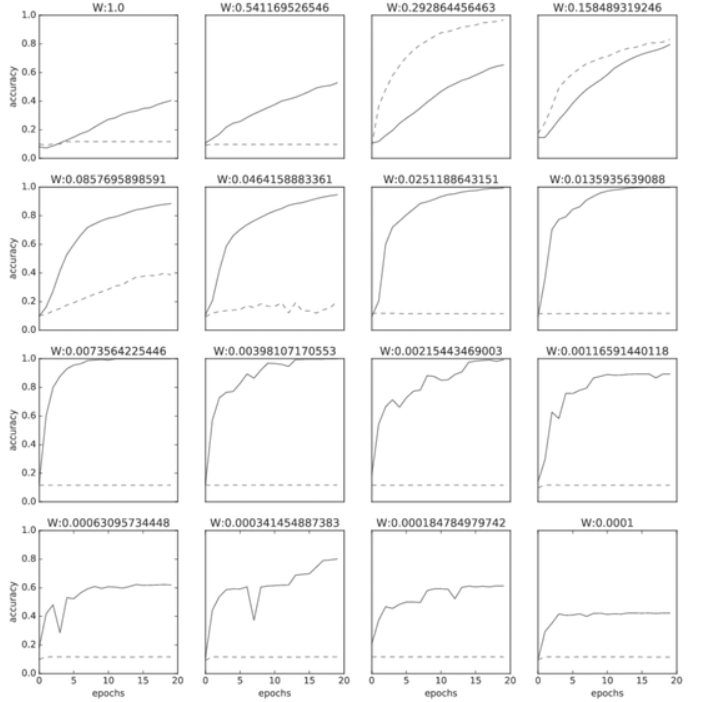
거의 모든 경우에서 배치 정규화를 사용할 때의 학습 진도가 빠른 것으로 나타납니다.
실제로 배치 정규화를 이용하지 않는 경우엔 초깃값이 잘 분포되어 있지 않으면 학습이 전혀 진행되지 않는 모습도 확인할 수 있습니다.
지금까지 살펴본 것처럼 배치 정규화를 사용하면 학습이 빨라지며, 가중치 초깃값에 크게 의존하지 않아도 됩니다.
'수학 > 딥러닝 이론' 카테고리의 다른 글
| [딥러닝] 2. 오버피팅 억제법 - 가중치 감소 (0) | 2020.10.03 |
|---|---|
| [딥러닝] 1. 오버피팅(과적합)이란? (0) | 2020.10.03 |
| [딥러닝] 3. 가중치의 초깃값 - ReLU를 사용할 때의 가중치 초깃값 - He 초깃값 (0) | 2020.10.03 |
| [딥러닝] 2. 가중치의 초깃값 - 가중치의 초깃값에 따라 은닉층의 활성화값 분포 변화, Xavier 초깃값 (2) | 2020.10.02 |
| [딥러닝] 1. 가중치의 초깃값 - 초깃값을 0으로 하면? (0) | 2020.10.02 |