최적의 모델 선택(Choosing the Optimal Model)
최상의 부분 집합 선택, 전진 선택, 후진 선택으로 모델의 집합을 생성합니다. 모델의 집합 중에 어느 모델이 최고의 성능을 갖고 있는지 판단해야 합니다. RSS가 가장 낮은 모델을 선택하거나, R2값이 가장 큰 모델을 선택하는 것은 training error와 연관되어 있으므로 부정확합니다. 따라서 test error가 낮은 모델을 선택해야 합니다.
test error를 측정하는 방법은 (1) 과적합으로 인한 편상을 고려하도록 훈련오차를 조정하여 test error를 간접적으로 추정할 수 있습니다. (2) validation set approach 또는 cross-validation approach를 사용하여 test error를 직접 추정합니다.
Cp, AIC, BIC, Adjusted R2
일반적으로 training set에 대한 MSE는 test MSE를 과소 추정합니다. training error와 관련된 RSS와 R2는 모델 선택에 적합하지 않습니다.
모델을 선택하기 위한 Cp, AIC(Akaike information criterion), BIC(Bayesian information criterion), adjusted R2 방법을 살펴보겠습니다.

(1) Cp
d개의 변수를 갖고 있는 적합된 최소 제곱 모델에 대하여 test MSE의 Cp는 다음 식을 사용하여 계산합니다.

위 식에서 시그마는 각 response에 대한 error의 분산을 의미하고, d는 predictor의 수를 의미합니다. training error는 test error를 과소평과 하기 때문에 2d$\sigma^2$만큼 패너티를 가합니다. d가 많아질수록 train RSS가 작아지므로 페널티는 더 크게 가합니다. Cp가 낮은 값을 갖는 모델이 best 모델 집합입니다.
(2) AIC(Akaike information criterion)
AIC는 최대가능도에 의해 적합한 모델의 큰 클래스에 의해 정의됩니다. 가우시안 error를 지닌 모델의 경우에 최대 가능도와 최소 제곱은 동일합니다. AIC는 다음과 같이 계산합니다.

Cp와 AIC의 식은 서로 비례합니다.
(3) BIC(Bayesian information criterion)
BIC는 베이지안 관점으로 유도됩니다. 그리고 Cp 또는 AIC와 비슷합니다. d개의 변수를 지닌 최소제곱 모델에 대하여 BIC는 다음과 같이 계산합니다.
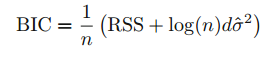
BIC값이 작은 모델이 best model 입니다. Cp에서 2d$\sigma^2$가 log(n)$\sigma^2$로 대체됩니다. n은 관측값의 수를 의미하며, n > 7인 경우에 BIC는 Cp보다 높은 패널티를 부여합니다.
(4) Adjusted R2
adjusted R2는 서로 다른 변수를 포하하는 모델 집합을 선택하는 유명한 방법입니다. R2는 1-Rss/TSS로 정의되었습니다. RSS는 모델에 변수가 추가될 때마다 감소하기 때문에, 변수가 추가되면 R2는 항상 증가했습니다. d개의 변수를 지닌 최소제곱 모델에서 adjusted R2는 다음과 같이 계산합니다.

Adjusted R2 큰 값이 small test error를 의미합니다. RSS는 변수가 추가되면 항상 감소하지만, RSS/(n-d-1)은 d 인자의 존재 때문에, 변수의 수에 따라 증가하기도 감소하기도 합니다. 모델에 noise 변수가 추가되면 d가 증가하게 되어 RSS/(n-d-1)값은 감소하게 되므로 adjusted R2는 감소합니다. 그러므로 가장 높은 adjusted R2는 noise가 없는 변수로 올바른 변수로만 구성된 모델을 의미합니다.
검증 및 교차검증(Validation and Cross-Validation)
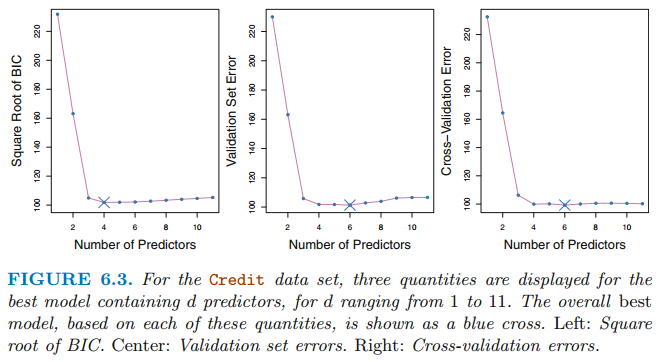
검증 및 교차검증은 test error를 직접 추정합니다. 각 모델에 대하여 validation set error또는 cross-validation eoor를 계산합니다. 그리고나서 test error가 가장 작은 모델을 선택합니다. 이 방법은 모델의 설명변수의 수를 정확히 알아내기 어렵거나 오차의 분산 $\sigma^2$를 정확히 추정하기 어려운 경우 사용합니다.
위 그리을 보면 4~10 변수를 가진 모델에 대하여 test error가 비슷합니다. validation and cross-validation 방법은 one-standard-error rule을 적용합니다. one-standard-error rule은 1 표준 오차이내에 있는 test eorrr에 따라 가장 크기가 작은 모델을 선택하는 것입니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 라쏘(Lasso) (0) | 2021.05.31 |
|---|---|
| [ISLR] 수축법(Shrinkage Methods), 능형 회귀(Ridge regression) (1) | 2021.05.31 |
| [ISLR] 부분집합 선택(Subset Selection), 최상의 부분 집합, 전진 단계적, 후진 단계적, 하이브리드 (0) | 2021.05.30 |
| [ISLR] 교차검증(Cross-validation), K-Fold, LOOCV (0) | 2021.05.09 |
| [ISLR] Classification - Logistic Regression, LDA, QDA, KNN (0) | 2021.05.08 |