반응형
Classification
분류는 범주형 자료를 다룹니다. 더미 변수를 활용하면 범주형 자료를 선형 회귀로도 풀 수 있지만, X의 범위가 제한되지 않고 Y값을 확률로 출력하지 않는 문제점이 있습니다.
1. 로지스틱 회귀(Logistic Regression)
p(X) 확률을 logistic function을 사용합니다.

최대 가능도가 높은 값을 갖는 계수 B0, B1을 추정합니다.

X가 2개 이상일 때는 다음과 같이 확장할 수 있습니다.
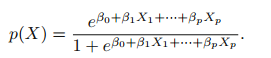
특징
- 결정 경계를 선형으로 예측합니다.
- X의 분포가 가우시안이 아닌 경우에 LDA보다 좋은 성능을 나타냅니다.
- 출력값을 확률로 나타낼 수 있습니다.
- Y가 2개 이상인 경우에 LDA를 주로 사용합니다.
2. 선형 판별 분석(LDA, Linear Discriminant Analysis)
특징
- 베이즈안 분류기를 근사화하는 모델입니다.
- Y가 2개 이상인 경우 로지스틱 회귀 대신에 사용합니다.
- 결정 경계를 선형으로 근사화 합니다.
- X의 분포를 가우시안으로 가정합니다.
- 사전 확률, K class에 속하는 K개의 X 평균, 분산을 추정하여 사후 확률을 계산합니다.
- 분산은 모두 동일하다고 가정합니다.
LDA는 사후 확률을 계산합니다.
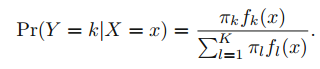
가능도 함수 P(XlY)를 가우시안으로 가정합니다.

사전 확률은 X가 Y에 속하는 비율을 계산합니다.
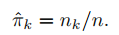
평균과 분산은 아래와 같이 추정합니다.

3. 이차 판별 분석(QDA, Quadratic Discriminant Analysis)
특징
- 결정 경계를 비선형으로 예측합니다.
- 사전 확률, k개 평균, k개 분산을 추정하여 사후 확률을 계산합니다.
- X 분포가 가우시안을 가정합니다.
4. K-최근접 이웃(KNN, K-nearest neighbors)
특징
- 비모수적 방법
- K에 따라 flexble 정도를 결정
5. 파이썬 구현
코드 출처: github.com/JWarmenhoven/ISLR-python
JWarmenhoven/ISLR-python
An Introduction to Statistical Learning (James, Witten, Hastie, Tibshirani, 2013): Python code - JWarmenhoven/ISLR-python
github.com
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.linear_model as skl_lm
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.metrics import confusion_matrix, classification_report, precision_score
from sklearn import preprocessing
from sklearn import neighbors
import statsmodels.api as sm
import statsmodels.formula.api as smf
%matplotlib inline
plt.style.use('seaborn-white')
데이터셋 불러오기
# 깃허브를 클론합니다.
!git clone https://github.com/emredjan/ISL-python
df = pd.read_csv('/content/ISL-python/datasets/Default.csv')
# factoriza()는 2개의 객체를 반환합니다.
# label array, 특정 값을 지닌 array
# 여기서는 label array에만 관심이 있습니다.
df['default2'] = df.default.factorize()[0]
df['student2'] = df.student.factorize()[0]
df.head(3)
설명 변수와 반응 변수 시각화
- 설명 변수: balance, income
- 반응 변수: default
# 설명 변수: balance, income
# 반응 변수: default
fig = plt.figure(figsize=(12,5))
gs = mpl.gridspec.GridSpec(1,4)
ax1 = plt.subplot(gs[0,:-2])
ax2 = plt.subplot(gs[0,-2])
ax3 = plt.subplot(gs[0,-1])
# default = no인 sample 추출
df_no = df[df.default2 == 0].sample(frac=0.15)
# default = yse인 sample 추출
df_yes = df[df.default2==1]
df_ = df_no.append(df_yes)
# 산점도
ax1.scatter(df_[df_.default == 'Yes'].balance, df_[df_.default == 'Yes'].income, s=40, c='orange', marker='+', linewidth=1)
ax1.scatter(df_[df_.default == 'No'].balance, df_[df_.default == 'No'].income, s=40, marker='o', linewidths='1',
edgecolors='lightblue', facecolors='white', alpha=.6)
ax1.set_ylim(ymin=0)
ax1.set_ylabel('Income')
ax1.set_xlim(xmin=-100)
ax1.set_xlabel('Balance')
# 박스 상자
c_palette = {'No':'lightblue', 'Yes':'orange'}
sns.boxplot('default', 'balance', data=df, orient='v', ax=ax2, palette=c_palette)
sns.boxplot('default', 'income', data=df, orient='v', ax=ax3, palette=c_palette)
gs.tight_layout(plt.gcf())
4.3 로지스틱 회귀
- 선형 회귀와 로지스틱 회귀 비교
X_train = df.balance.values.reshape(-1,1)
y = df.default2
# test data 배열 생성
# classification 확률과 class 예측값을 계산
X_test = np.arange(df.balance.min(), df.balance.max()).reshape(-1,1)
clf = skl_lm.LogisticRegression(solver='newton-cg') # 로지스틱 회귀
clf.fit(X_train,y) # 계수 예측
prob = clf.predict_proba(X_test) # X_test에 대한 확률 계산
fig, (ax1, ax2) = plt.subplots(1,2,figsize=(12,5))
# 왼쪽 plot, 선형 회귀
sns.regplot(df.balance, df.default2, order=1, ci=None,
scatter_kws={'color':'orange'},
line_kws={'color':'lightblue', 'lw':2}, ax=ax1)
# 오른쪽 plot, 로지스틱 회귀
ax2.scatter(X_train, y, color='orange')
ax2.plot(X_test, prob[:,1], color='lightblue')
for ax in fig.axes:
ax.hlines(1, xmin=ax.xaxis.get_data_interval()[0],
xmax=ax.xaxis.get_data_interval()[1], linestyles='dashed', lw=1)
ax.hlines(0, xmin=ax.xaxis.get_data_interval()[0],
xmax=ax.xaxis.get_data_interval()[1], linestyles='dashed', lw=1)
ax.set_ylabel('Probability of default')
ax.set_xlabel('Balance')
ax.set_yticks([0, 0.25, 0.5, 0.75, 1])
ax.set_xlim(xmin=-100)
로지스틱 회귀 통계값
- 설명 변수: balance
- 반응 변수: default
y = df.default2
clf = skl_lm.LogisticRegression(solver='newton-cg') # 로지스틱 회귀 수행
X_train = df.balance.values.reshape(-1,1) # balance
clf.fit(X_train,y) # 계수 예측
print(clf)
print('classes: ', clf.classes_)
print('coefficients: ', clf.coef_)
print('intercept :',clf.intercept_)
X_train = sm.add_constant(df.balance)
est = sm.Logit(y.ravel(), X_train).fit()
est.summary2().tables[1]
- 설명 변수: student
- 반응 변수: default
X_train = sm.add_constant(df.student2)
y = df.default2
est = sm.Logit(y, X_train).fit()
est.summary2().tables[1]
다중 로지스틱 회귀
- 설명 변수: balance, income, student
- 반응 변수: default
X_train = sm.add_constant(df[['balance', 'income', 'student2']])
est = sm.Logit(y,X_train).fit()
est.summary2().tables[1]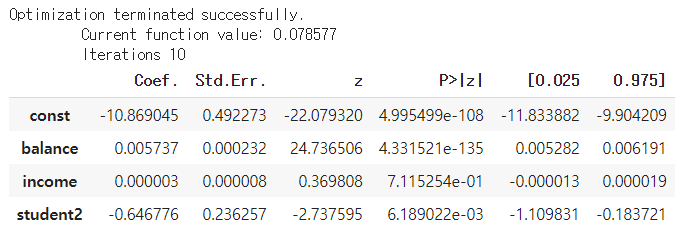
교란(Confounding)
# student에 대한 balance와 default
X_train = df[df.student == 'Yes'].balance.values.reshape(df[df.student=='Yes'].balance.size,1)
y = df[df.student == 'Yes'].default2
# non-student에 대한 balance와 default
X_train2 = df[df.student == 'No'].balance.values.reshape(df[df.student == 'No'].balance.size,1)
y2 = df[df.student == 'No'].default2
X_test = np.arange(df.balance.min(), df.balance.max()).reshape(-1,1)
clf = skl_lm.LogisticRegression(solver='newton-cg')
clf2 = skl_lm.LogisticRegression(solver='newton-cg')
clf.fit(X_train,y)
clf2.fit(X_train2,y2)
prob = clf.predict_proba(X_test)
prob2 = clf2.predict_proba(X_test)
df.groupby(['student', 'default']).size().unstack('default')
# 시각화
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(12,5))
# 왼쪽 plot
ax1.plot(X_test, pd.DataFrame(prob)[1], color='orange', label='Student')
ax1.plot(X_test, pd.DataFrame(prob2)[1], color='lightblue', label='Non-student')
ax1.hlines(127/2817, colors='orange', label='Overall Student',
xmin=ax1.xaxis.get_data_interval()[0],
xmax=ax1.xaxis.get_data_interval()[1], linestyles='dashed')
ax1.hlines(206/6850, colors='lightblue', label='Overall Non-Student',
xmin=ax1.xaxis.get_data_interval()[0],
xmax=ax1.xaxis.get_data_interval()[1], linestyles='dashed')
ax1.set_ylabel('Default Rate')
ax1.set_xlabel('Credit Card Balance')
ax1.set_yticks([0, 0.2, 0.4, 0.6, 0.8, 1.])
ax1.set_xlim(450,2500)
ax1.legend(loc=2)
# 오른쪽 plot
sns.boxplot('student', 'balance', data=df, orient='v', ax=ax2, palette=c_palette);
4.4 선형 판별 분석(LDA, Linear Discriminant Analysis)
X = df[['balance', 'income', 'student2']]
y = df.default2
# 선형 판별 분석
lda = LinearDiscriminantAnalysis(solver='svd')
y_pred = lda.fit(X, y).predict(X)
df_ = pd.DataFrame({'True default status': y,
'Predicted default status': y_pred})
df_.replace(to_replace={0:'No', 1:'Yes'}, inplace=True)
df_.groupby(['Predicted default status','True default status']).size().unstack('True default status')
print(classification_report(y, y_pred, target_names=['No', 'Yes']))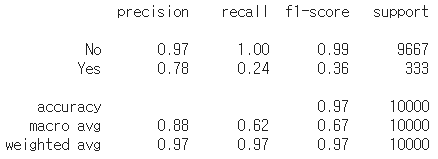
사후 확률 임계값 낮추기
decision_prob = 0.2
y_prob = lda.fit(X, y).predict_proba(X)
df_ = pd.DataFrame({'True default status': y,
'Predicted default status': y_prob[:,1] > decision_prob})
df_.replace(to_replace={0:'No', 1:'Yes', 'True':'Yes', 'False':'No'}, inplace=True)
df_.groupby(['Predicted default status','True default status']).size().unstack('True default status')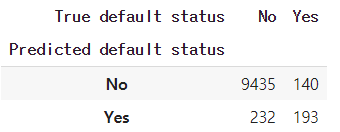
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
반응형
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 수축법(Shrinkage Methods), 능형 회귀(Ridge regression) (1) | 2021.05.31 |
|---|---|
| [ISLR] Cp, AIC, BIC, Adjusted R2, 검증 및 교차검증(Validation and Cross-Validation) (0) | 2021.05.30 |
| [ISLR] 부분집합 선택(Subset Selection), 최상의 부분 집합, 전진 단계적, 후진 단계적, 하이브리드 (0) | 2021.05.30 |
| [ISLR] 교차검증(Cross-validation), K-Fold, LOOCV (0) | 2021.05.09 |
| [ISLR] 선형 회귀(Linear Regression) Python코드 (1) | 2021.05.03 |