반응형
차원축소 방법(Dimension Reduction Methods)
차원축소 방법은 p개의 변수 X1, X2, ... ,Xp를 변환하여, 변환된 변수들로 선형제곱 모델을 적합(fit)하는 것입니다. p개의 X1~Xp에서 m개의 Z1~Zm으로 변환된 변수들은 X1~Xp의 선형 결합으로 나타냅니다.
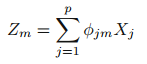
변환된 변수들로 다음과 같이 최소제곱 모델을 fit할 수 있습니다.

이러한 차원축소 방법은 일반적으로 선형제곱 모델보다 뛰어납니다. 차원축소 방법은 기존의 p+1(절편 포함)개의 변수를 m+1개의 변수로 축소하기 때문입니다. 변수의 수가 줄어들었으므로 bias를 증가시키고 variance를 감소합니다. 즉, overfitting을 방지합니다. 이전에 살펴보았던 변수 선택 방법과 수축법과 비슷한 효과를 나타냅니다.
차원축소 방법에서 각 변수들과 계수 추정치는 다음과 같이 나타낼 수 있습니다.


따라서 차원축소 방법은 최소제곱 방법의 계소 추정치를 제한하는 역할을 합니다. 이러한 형태의 제한은 계수추정치가 편향되도록 합니다.
차원축소 방법은 다음과 같은 과정으로 진행됩니다. (1) 변환된 m개의 변수 Z1~Zm를 얻습니다. (2) m개의 변수들을 사용하여 모델을 fit합니다. 다음 포스팅에서는 차원축소 방법중 하나인 주성분 회귀(principal components regression)을 살펴보겠습니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
반응형
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 주성분 회귀(PCR, Principal Components Regression) (0) | 2021.06.05 |
|---|---|
| [ISLR] 주성분 분석 개요(Overview of Prinicipal Components Analysis) (0) | 2021.06.05 |
| [ISLR] 라쏘(Lasso)와 능형 회귀(Ridge regression) 비교 (0) | 2021.06.01 |
| [ISLR] 라쏘(Lasso) (0) | 2021.05.31 |
| [ISLR] 수축법(Shrinkage Methods), 능형 회귀(Ridge regression) (1) | 2021.05.31 |