차원축소 방법 중 하나인 주성분 회귀를 알아보겠습니다. 차원축소 방법을 간단히 살펴보면 p개의 변수를 m개의 변수로 축소하여 bias를 증가시키고 variance를 감소합니다. 따라서 overfitting을 방지하는 효과가 있습니다.
주성분 회귀(Principal Components Regression)
주성분분석(PCA, Principal Components Analysis)는 변수의 큰 집합으로부터 저차원의 특징을 유도하기 위한 유명한 방법입니다. PCA는 비지도학습의 방법이며, 여기서는 회귀를 위한 차원축소 방법으로서 PCA를 사용하는 것을 살펴보겠습니다. 주성분 회귀를 알아보기 전에 주성분분석을 잠깐 살펴보겠습니다.
주성분분석 개요(An Overview of Principal Components Analysis)
주성분 회귀를 공부하기 전에 주성분분석이 무엇인지 알아보겠습니다.
PCA는 nxp 데이터 행렬 X의 차원을 감소하기 위한 방법입니다. 데이터의 첫 번째 주성분 요소 방향은 관측값들이 가장 크게 변화하는 방향입니다.

위 그림에서 초록색 선은 데이터의 첫 번째 주성분 요소 방향을 나타냅니다. 이 방향으로 데이터가 가장 큰 변동성을 갖는 다는 것을 확인할 수 있습니다. 즉, 모든 데이터를 첫 번째 주성분 요소 방향으로 사영(projection)하면 가장 큰 분산을 갖습니다. 다른 방향으로 사영한다면 이보다 적은 분산을 갖습니다. 점을 선에 사영하는 것은 선 위에서 점과 가장 가까운 위치를 찾는 것을 의미합니다.
첫 번째 주성분 요소 방향은 위 그림에서 시각적으로 나타냈지만, 어떻게 수학적으로 표현할 수 있을까요?


0.839와 0.544는 principal component loading이며, 방향을 정의합니다. 또한 각 주성분 loading의 l2 norm은 1인 것을 고려해야 합니다. 그렇지 않으면 아주 큰 분산을 만들수 있습니다.

또한 첫 번째 주성분 요소 식에서의 선형 결합은 가장 큰 분산을 생성합니다. 예를 들어, 아래의 식이 최대화 됩니다.
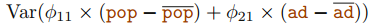
첫 번째 주성분 점수(principal component scores)는 다음과 같이 정의됩니다.
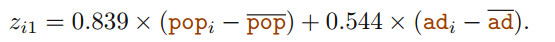

PCA는 또한 다르게 해석될 수 있습니다. 첫 번째 주성분 요소 벡터는 데이터와 가장 가까운 선을 정의합니다. 예를 들어 첫 번째 주성분 직선은 각 점과 선 사이의 직교 거리의 제곱 합을 최소로 합니다. 첫 번째 주성분은 투영된 관측치들이 원래의 관측치들에 가능한 한 가깝도록 선택됩니다.
주성분 점수는 두 변수를 하나의 값으로 표현하는데 두 변수를 잘 표현할 까요? 위 예제에서 pop과 ad는 선형 관계를 갖으므로 하나의 값은 두 변수를 잘 요약한다고 기대할 수 있습니다.
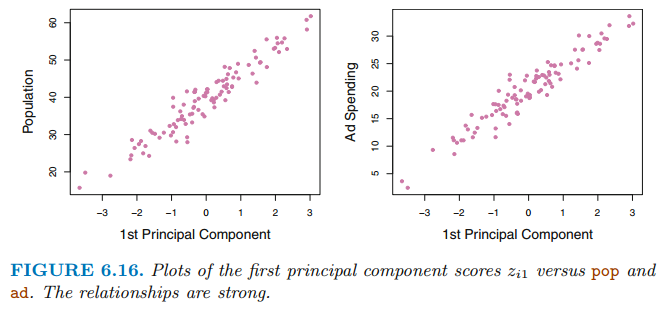
위 그림은 첫 번째 주성분 점수 $z_{i1}$과 pop, ad 사이의 관계를 시각화 한 것입니다. 그림을 살펴보면 주성분 요소와 두 변수 사이에 강한 관계가 있음을 나타냅니다. 다른말로하면 첫 번째 주성분 요소는 pop과 ad가 포함하고 있는 대부분의 정보를 포착한다고 생각할 수 있습니다.
지금까지 첫 번째 주성분 요소만을 살펴보았습니다. 일반적으로 주성분은 p개 까지 구할 수 있습니다. 이제 두 번째 주성분 요소 Z2를 살펴보겠습니다. Z2도 Z1과 마찬가지로 두 변수의 선형결합으로 이루어져 있으며 Z1과 관계가 없습니다. 각 주성분 요소 방향은 서로 orthogonal 이므로 독립적입니다. Z2는 Z1을 제외하고 가장 큰 분산을 갖는 변수들의 선형결합입니다. 두 번째 주성분 요소는 다음과 같이 주어집니다.


위 그림을 살펴보면 두 번쨰 주성분 요소 점수는 0에 가까우며 이는 더 적은 정보를 포착한다는 것을 나타냅니다.

위 그림은 두 번째 주성분 요소와 pop, ad를 시각화 한 것입니다. 두 번째 주성분 요소와 두 변수 사이의 관계가 미약하다는 것을 알 수 있습니다. 이 예제에서는 2가지 변수만을 갖으므로 주성분 요소를 2개까지만 구할 수 있습니다. 또한 주성분들은 앞의 주성분들과 상관관계가 없다는 제한조건 하에서 분산을 최대로 합니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 부분 최소 제곱(PLS, Partial Least Squares) (0) | 2021.07.21 |
|---|---|
| [ISLR] 주성분 회귀(PCR, Principal Components Regression) (0) | 2021.06.05 |
| [ISLR] 차원축소 방법(Dimension Reduction Methods) (0) | 2021.06.01 |
| [ISLR] 라쏘(Lasso)와 능형 회귀(Ridge regression) 비교 (0) | 2021.06.01 |
| [ISLR] 라쏘(Lasso) (0) | 2021.05.31 |