부분 최소 제곱(PLS, Partial Least Squares)
부분 최소 제곱(PLS)는 PCR(주성분 회귀)의 supervised alternative 입니다. PLS는 기존 특징의 선형 결합으로 이루어진 새로운 특징 집합 ($Z_1, ... , Z_M$)을 식별합니다. 그리고나서 이 M개의 특징을 사용하여 최소 제곱 방법을 통해 선형 모델을 적합(fit) 합니다. PCR과 가장 큰 차이점은 supervised way 라는 것입니다.
반응 변수 Y를 사용하여 새로운 특징들을 식별하기 때문에 기존 특징들을 잘 설명할 뿐만아니라 반응 변수와 연관성이 있습니다. 즉, PLS는 반응 변수와 설명 변수 사이를 설명하는 방향을 찾습니다.
우선, p개의 설명 변수들을 standardizing 한 후에, 기존 변수들 각각에 가중치를 가하여 선형 결합한 첫 번째 방향 $Z_1$을 계산합니다. 반응 변수와 가장 상관성있는 설명 변수에 높은 가중치를 부여합니다.
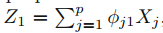
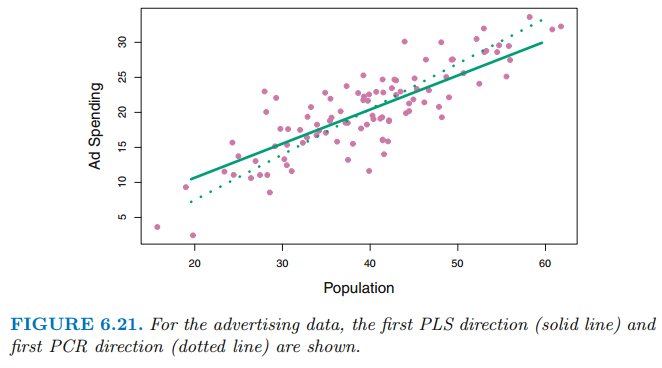
직선이 PLS 방향인데, population 변화에 따른 Ad spending에 less sensitive한 모습을 보여줍니다. 이는 ad spending보다 population 이 더 높은 상관관계를 갖고 있다는 것을 의미합니다.
두 번째 PLS 방향을 식별하기 위하여 $Z_1$의 각 변수에 회귀를 하고 잔차를 취하여 $Z_1$에 대한 각 변수들을 조정합니다. 이 잔차들은 첫 번째 PLS 방향에의해 설명되지 않는 남아있는 정보로 해석할 수 있습니다. 그리고나서 직교화된 데이터로 $Z_2$를 $Z_1$과 같은 방법으로 계산합니다. 이 과정을 M번 반복하여 PLS의 요소 $Z_1, ... Z_M$를 식별합니다. 마지막으로 $Z_1 ~ Z_M$을 사용하여 Y를 예측하기 위해 선형 모델을 최소 제곱법으로 적합 합니다.
식별된 M개의 변수들은 교차검증에 의해 선택되는 조율 파라미터 입니다. 일반적으로 PLS 방법은 PCR 또는 능형 회귀와 비슷한 성능을 보입니다. PLS의 supervised 차원 축소 방법은 bias를 감소시킬 수 있는 반면에 variance를 증가시킬 수 있습니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 계단 함수(Step Functions) (0) | 2021.07.25 |
|---|---|
| [ISLR] 다항식 회귀(Polynomial Regression) (0) | 2021.07.25 |
| [ISLR] 주성분 회귀(PCR, Principal Components Regression) (0) | 2021.06.05 |
| [ISLR] 주성분 분석 개요(Overview of Prinicipal Components Analysis) (0) | 2021.06.05 |
| [ISLR] 차원축소 방법(Dimension Reduction Methods) (0) | 2021.06.01 |