다항식 회귀(Polynomial Regression)
반응 변수(Y, response)와 설명 변수(X, predictors) 사이의 관계가 비선형인 상황에서 선형 회귀(Linear Regression)을 확장하는 방법은 다항식 함수(polynomial function)으로 대체하는 것입니다.
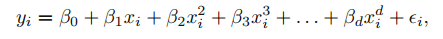
이 방법이 다항식 회귀이며 차수 d가 충분히 큰 경우에 다항식 회귀는 비선형 곡선을 나타냅니다. 위 식에서 계수들은 최소 제곱을 사용하여 쉽게 추정될 수 있습니다.
d 가 3 또는 4보다 큰 경우에 다항 회귀는 과하게 flexible한 곡선을 만듭니다. 이 경우에 과적합이 발생할 수 있습니다.

위 그림은 나이에 따른 임금 데이터에서 차수가 4인 다항 회귀를 최소 제곱을 사용하여 적합한 결과입니다. 점선으로 된 곡선들은 2x 표준오차 곡선들입니다. 나이가 x0인 값에서 적합을 계산한다고 가정하겠습니다.

최소 제곱은 적합된 계수 $\beta$ 각각에 대하여 분산 추정치들과 계수 추정치 쌍들 사이에 공분산을 제공합니다. 이것들의 사용하여 f(x)의 추정 분산 Var(f(x0))을 계산할 수 있습니다. f(x0)의 추정된 점별(pointwise) 표준 오차는 분산의 제곱근 입니다. 이 계산을 각 기준점 x0에서 반복하여 적합된 곡선과 적합된 곡선의 양쪽에 표준오차 2배 값을 그래프로 나타냅니다. 표준오차의 2배를 그래프로 나타내는 이유는 이 값이 정구 분포의 오차항들에 대해 95% 신뢰 구간을 제공하기 때문입니다.
위 데이터에서 고소득자와 저소득자 그룹으로 구분할 수 있는데 이 이진 반응 변수를 예측하기 위하여 로지스틱 회귀를 사용할 수 있습니다.

위 자료의 표본 크기는 상당히 크지만(n=3000), 고소득자는 79명 뿐입니다. 이 때문에 추정된 계수들의 분산이 높고 그 결과 신뢰구간이 넓습니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 회귀 트리(Regression Trees) (0) | 2021.07.28 |
|---|---|
| [ISLR] 계단 함수(Step Functions) (0) | 2021.07.25 |
| [ISLR] 부분 최소 제곱(PLS, Partial Least Squares) (0) | 2021.07.21 |
| [ISLR] 주성분 회귀(PCR, Principal Components Regression) (0) | 2021.06.05 |
| [ISLR] 주성분 분석 개요(Overview of Prinicipal Components Analysis) (0) | 2021.06.05 |