회귀 트리(Regression Tree)
의사결정트리(decision tree)는 회귀와 분류 문제를 풀 수 있습니다. 그 중에서 회귀 문제를 어떻게 푸는지 살펴보겠습니다.

위 그림은 야구 선수들의 경력과 안타 수에 따른 연봉 데이터셋에 대해 예측을 수행하기 위한 회귀 트리 입니다. 트리의 맨 위는 years<4.5 에따라 분할됩니다. 설명 변수의 공간이 여러 수의 간단한 구역으로 분할되는 것입니다. 위 그림은 3가지 구역으로 분할되어 있습니다. 그리고 예측 값은 관측값이 속간 구역에 대하여 모든 설명변수들의 평균값으로 예측합니다.

위 그림은 트리가 분할한 세 가지 구역을 나타냅니다. 결정 트리(decision tree)는 위에서 아래로 나아가고 구역들 R1, R2, R3는 종단 노드(terminal node) 또는 잎(leaves)라고 부릅니다. 설명 변수 공간이 분할되는 부분은 내부 노드(internal nodes), 노드를 연결하는 트리 부분은 가지(branch)라고 합니다.
회귀 트리는 변수들의 관계를 단순화하여 보여주어 해석이 쉽고 그래픽으로 표현하기 쉽습니다.
회귀 트리를 어떻게 만드는지 살펴보겠습니다.
1. 설명 변수 공간을 분할합니다. X1~Xp p개의 설명 변수를 J개의 서로 다른 겹치치 않는 구역 R1~Rj로 분할합니다.
2. 구역 Rj에 속하는 모든 관측값들에 평균값을 취해 동일한 예측값을 갖도록 합니다.
그러면 구역을 어떻게 분할해야 할까요?? 아래의 RSS를 최소화하는 방향으로 구역 R1 ~ Rj를 찾습니다.

$\hat{y}_{R_j}$는 j 구역에 있는 모든 관측값들의 평균값 입니다. 하지만 모든 구역에 대하여 이를 계산하는 것은 불가능에 가깝습니다. 이러한 이유로 재귀이진분할(recursive binary splitting)로 알려진 하향식의 그리디 기법을 사용합니다. 트리의 맨 위에서 시작하여 예측공간을 연속하여 분할해 내려갑니다. 이 때 각 분할은 트리에서 ㅏㅇ래 방향으로 생성된 두 개의 새로운 가지로 표시됩니다.
재귀이진분할(recursive binary splitting)을 수행하기 위해 설명 변수 Xj를 선택하고 설명 변수 공간을 분할하기 위한 중단점 s를 선택합니다. s는 s에 의해 분할되는 공간이 RSS를 최소화해야하는 방향으로 선택합니다.
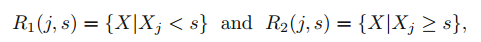

이러한 방식으로 구역을 계속 분할하는데, 일정한 중단 기준을 갖고 기준을 충족하면 분할을 중지할 수 있습니다. 예를 들어 각 구역에 관측값이 5개 이하가 될 때 까지 분할하기 등이 있습니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 분류 트리(Classification Tree) (0) | 2021.07.30 |
|---|---|
| [ISLR] Tree Pruning (0) | 2021.07.28 |
| [ISLR] 계단 함수(Step Functions) (0) | 2021.07.25 |
| [ISLR] 다항식 회귀(Polynomial Regression) (0) | 2021.07.25 |
| [ISLR] 부분 최소 제곱(PLS, Partial Least Squares) (0) | 2021.07.21 |