Tree Pruning

트리를 구축하는 과정에서 이전 포스팅에서 살펴본 재귀이진분할은 데이터에 과적합할 위험이 있습니다. 이러한 문제를 해결하기 위한 적합한 대안은 Pruning 입니다.
가장 큰 트리를 만든 다음에 이것을 prune하여 서브트리를 얻는 것입니다. 그러면 tree를 어떤 기준으로 pruning 해야 할까요?
직관적으로 subtree를 선택하는 목적은 가장 낮은 test error를 도출하는 것입니다. 주어진 subtree에 대하여 cross-validation 혹은 validation set apporach를 사용하여 test error를 계산할 수 있습니다. 하지만 모든 가능한 subtree에 대하여 CV하는 것은 불가능해보입니다. 대신에 subtree를 선택하는 방법을 살펴보겠습니다.
Cost complexity prunning or Weakest link pruning
모든 가능한 subtree를 고려하기보다 조율 파라미터 $\alpha$에 의한 tree sequence를 고려합니다. 각 $\alpha$에 대해 아래 식이 가능한 작게 하는 subtree가 있습니다.

T는 트리의 터미널 노드의 수(leaves)를 말합니다. 조율 파라미터 $\alpha$에 따라 터미널 노드수가 loss에 미치는 영향이 달라지며 $\alpha = 0$일 때 단순히 오차를 측정하기 때문에 서브트리는 전체 트리와 같습니다. $\alpha$가 큰 경우에 터미널 노드 수에따라 큰 error를 출력하므로 터미널 노드가 작을 때 최소로 되는 경향이 있습니다.
$\alpha$는 cross validation을 사용하여 선택할 수 있습니다. 그 후에 $\alpha$에 대응하는 subtree를 얻습니다. 이 과정은 다음의 알고리즘으로 수행됩니다.

위 트리는 9개의 feature를 사용했습니다. 무작위로 dataset을 절반으로 분할하여 회귀 트리를 형성합니다. 그리고 서로 다른 터미널 노드를 갖고 있는 서브트리를 생성하기 위해 $\alpha$를 변경합니다. 마지막으로 test MSE를 측정하기 위해 k-fold cross validation을 수행합니다.
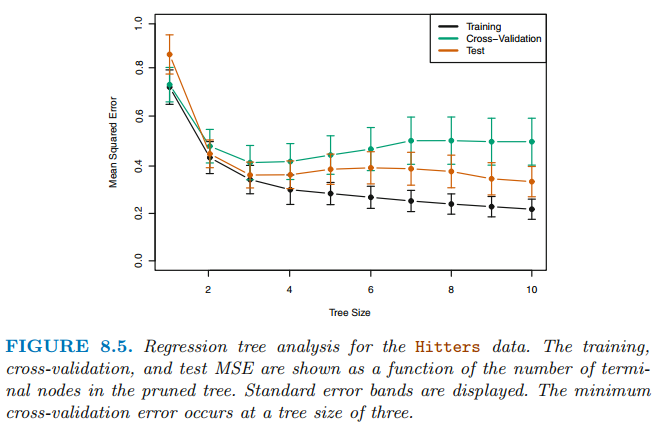
위 그림을 살펴보면 tree size가 3일 때 test error와 cross-validation error가 가장 낮습니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 트리와 선형 모델, 트리의 장단점 (0) | 2021.07.30 |
|---|---|
| [ISLR] 분류 트리(Classification Tree) (0) | 2021.07.30 |
| [ISLR] 회귀 트리(Regression Trees) (0) | 2021.07.28 |
| [ISLR] 계단 함수(Step Functions) (0) | 2021.07.25 |
| [ISLR] 다항식 회귀(Polynomial Regression) (0) | 2021.07.25 |