계단 함수(Step Functions)
X의 범위를 bins로 쪼개어 각 bin에 대한 서로 다른 상수로 적합합니다. 이는 연속 변수(continuous variable)을 순서범주형 범주(ordered categorical variable)로 전환합니다.
X의 범위에서 절단점(cut point)을 사용하여 K+1개의 새로운 변수를 생성합니다.

여기서 I는 지시 함수이며 조건이 참이면 1, 그렇지 않으면 0을 반환합니다. 이는 더미 변수(dummy variable)이라고도 부릅니다. 주의할 점은 어느 X에 대하여 $C_0(X) + C_1(X) + ... + C_K(X) = 1$을 만족합니다. X가 K+1 구간중 하나에만 속하기 때문입니다. 위 더미 변수를 설명 변수로 사용하여 선형 모델을 최소 적합할 수 있습니다.

주어진 X에 대하여 C1, C2, ... ,Ck중 하나의 값만 non-zero가 됩니다. 만약 X < c1 인 경우에 설명변수는 0입니다. 따라서 $\beta_0$은 X < c1에 대하여 Y의 평균값으로 해석할 수 있습니다.
위 식에서 $c_j <= X < c_{j+1}$에 대한 $beta_0 + \beta_j$는 $X < c_1$에 상대적인 $c_j <= X < c_{j_1}에 대한 반응 변수 평균 증가를 나타냅니다.
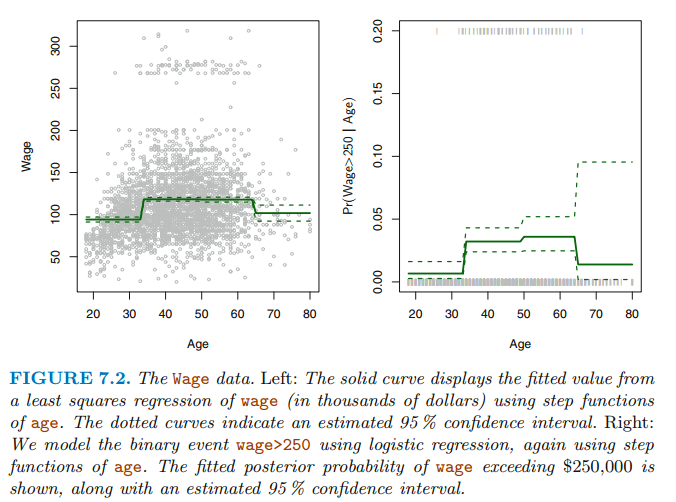
위 데이터셋은 고소득자와 저소득자 두 그룹으로 나뉘어져 있는데 이 이진 분류를 수행하기 위하여 로지스틱회귀를 사용할 수 있습니다.
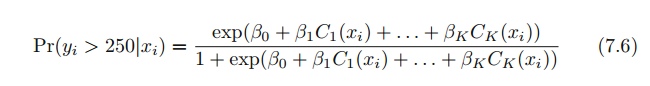
설명변수안에 중단점이 없다면 조각별 상수 함수는 변화를 놓칠 수 있습니다. 예를 들어 위 그림에서 왼쪽에서 첫 번째 bin은 age와 wage 사이의 상승하는 경향을 나타내지 못합니다. 이럼에도 계산 함수는 자주 쓰이는데 5년 간격의 기간을 설정하는 경우에 자주 사용합니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] Tree Pruning (0) | 2021.07.28 |
|---|---|
| [ISLR] 회귀 트리(Regression Trees) (0) | 2021.07.28 |
| [ISLR] 다항식 회귀(Polynomial Regression) (0) | 2021.07.25 |
| [ISLR] 부분 최소 제곱(PLS, Partial Least Squares) (0) | 2021.07.21 |
| [ISLR] 주성분 회귀(PCR, Principal Components Regression) (0) | 2021.06.05 |