라쏘와 능형 회귀의 또 다른 구성(Another Formulation for Ridge Regression and the Lasso)
이전 포스팅에서 살펴보았던 라쏘와 능형회귀가 다음의 문제를 푼다고 가정해보겠습니다.

위 식은 R1 + R2 <= s인 범위에 존재하는 모든 점들 중에 가장 낮은 RSS를 찾게 합니다. Lasso는 범위가 다이아몬드로 정의되고, ridge regression은 원으로 정의됩니다.

만약 s가 아주 크다면 기존의 최소제곱 추정치와 동일한 값을 출력할 것입니다. s가 매우 작다면 모든 계수들도 작은 값을 갖습니다.
아래와 같이 식을 수정하여 문제를 푼다면 원하는 변수의 수를 갖는 모델을 찾을 수 있습니다.
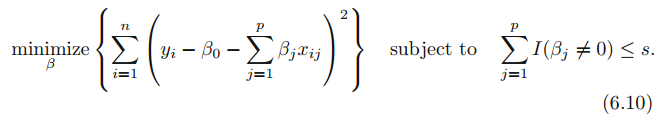
I는 지시 함수를 의미하며 반약 B 변수가 0이 아니면 1, B 변수가 0이면 0을 반환합니다. 즉, non zero 변수의 개수를 계산할 수 있습니다. 이 지시 함수의 결과값이 s보다 작도록 제약조건을 가하면 s개의 변수를 지닌 모델이 RSS가 낮아지는 방향으로 fit 하도록 할 수 있습니다. 이 방법은 best subset selection과 동일합니다. best subset selection은 p가 큰 경우에 계산량이 기하급수적으로 많아져 불가능 하므로 대안의 방법으로 제약조건을 가하는 것입니다.
라쏘와 능형 회귀 비교(Comparing the Lasso and Ridge Regression)
라쏘는 변수들의 부분 집합만을 포함하는 모델을 생성하여 더 간단하고 해석 가능하다는 점이 능형회귀와 비교하여 주된 장점입니다. 하지만 정확도는 어느 방법이 더 나을까요?

위 그림을 살펴보면 lasso와 ridge는 거의 비슷한 양상을 보입니다. 람다가 증가하면 variance는 감소하고, bias는 증가합니다. 오른쪽 그림을 좀 더 살펴보면, ridge regression의 variance가 lasso의 variance보다 낮고, bias는 거의 동일합니다. 위 예제는 45개의 변수가 모두 반응 변수와 연관되어 있는 경우입니다. 이 경우에 lasso는 변수들을 정확하게 0으로 만들으므로, ridge regression이 lasso보다 뛰어난 성능을 나타내는 것이 당연합니다. 다른 예제를 살펴보겠습니다.

위 예제는 단순히 2개의 변수만이 설명 변수와 관련있는 경우입니다. 이 경우에는 lasso가 bias, variance, MSE 모두 ridge regression을 능가합니다.
이 두 예제는 ridge regression와 lasso 중에 어느 방법이 항상 뛰어나지 않다는 것을 보여줍니다. 일반적으로 적은 수의 변수들이 반응 변수와 관련되어 있으면 lasso의 성능이 더 좋고, 많은 변수들이 반응 변수와 관련되어 있는 경우에는 ridge regression의 성능이 더 좋습니다. 하지만 얼만큼의 변수들이 반응 변수와 관련되어 있는지는 알기 어렵습니다. 따라서 어느 방법이 더 뛰어난지 알기 위해서는 cross-validation 방법을 사용해야 합니다.
능형 회귀와 라쏘에 대한 특별한 경우(A Simple Special Case for Ridge Regression and the Lasso)
문제를 간단히 하기 위해 절편을 없애고, n=p인 경우를 가정하겠습니다. 따라서 기존 최소제곱문제는 다음의 식을 최소화 하는 방향으로 계수를 추정합니다.

이 경우에 최소 제곱해는 다음과 같습니다.

ridge regression은 다음의 식을 최소화 하는 방향으로 계수를 추정합니다.

lasso는 다음의 식을 최소화하는 방향으로 계수를 추정합니다.

ridge regression은 다음과 같이 계수를 추정합니다.

lasso는 다음과 같이 계수를 추정합니다.

lasso와 ridge regression은 서로 다른 종류의 수축법을 수행하는 것을 확인할 수 있습니다. ridge regression에서 각 최소제곱 계수 추정치는 동일한 비율로 수축하고, lasso는 일정한 양만큼 계수들을 0으로 수축합니다. 이 것을 soft-thresholding이라고 부릅니다. lassos는 계수들을 0으로 수축하므로 변수 선택을 수행한다고 생각할 수 있습니다.

위 그림을 살펴보면 ridge regression은 동일한 비율로 계수를 수축하고, lasso는 동일한 양으로 계수를 수축하는 것을 확인할 수 있습니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 주성분 분석 개요(Overview of Prinicipal Components Analysis) (0) | 2021.06.05 |
|---|---|
| [ISLR] 차원축소 방법(Dimension Reduction Methods) (0) | 2021.06.01 |
| [ISLR] 라쏘(Lasso) (0) | 2021.05.31 |
| [ISLR] 수축법(Shrinkage Methods), 능형 회귀(Ridge regression) (1) | 2021.05.31 |
| [ISLR] Cp, AIC, BIC, Adjusted R2, 검증 및 교차검증(Validation and Cross-Validation) (0) | 2021.05.30 |