(밑바닥부터 시작하는 딥러닝, 사이토 고키)을 바탕으로 작성하였습니다.
신경망 - Neural Network
이전 포스팅에서는 퍼셉트론에 대하여 설명하였습니다.
이번 포스팅에서는 3층 신경망 순전파를 구현해보면서 신경망에 대해 알아보겠습니다.
순전파는 입력부터 출력까지의 과정을 의미합니다.
퍼셉트론에서는 AND, OR 게이트의 진리표를 보면서 사람이 적절한 가중치 값을 정했습니다.
신경망은 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습할 수 있습니다.
1. 퍼셉트론에서 신경망으로
1.1 신경망의 예
신경망을 그림으로 나타내면 다음과 같이 됩니다. 입력층, 은닉층, 출력층으로 나뉘어져 있습니다.

1.2 퍼셉트론 복습
$x_{1}$과 $x_{2}$라는 두 신호를 입력받아 y를 출력하는 퍼셉트론을 수식으로 나타내면 다음과 같습니다.

여기서 편향을 명시한다면 다음과 같이 나타낼 수 있습니다.

위 퍼셉트론의 동작 원리
1. $x_{1}$, $x_{2}$, 1 이라는 3개의 신호가 뉴런에 입력됩니다.
2. 각 신호에 가중치를 곱한 후, 다음 뉴런에 전달됩니다.
3. 다음 뉴런에서 신호의 값을 더하여, 그 합이 0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력합니다.
함수 $h(x)$를 정의하면 더 간결한 형태로 작성할 수 있습니다.
$h(x)$는 동작(0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력)을 의미합니다.

1.3 활성화 함수의 등장
활성화 함수는 $h(x)$와 같이 입력 신호의 총합을 출력 신호로 변환하는 함수입니다. 활성화 함수는 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 합니다.

a는 가중치가 달린 입력신호와 편향의 총합을 계산합니다.
a를 함수 $h()$에 넣어 y를 출력합니다.
뉴런과 노드를 같은 의미로 사용합니다.
2. 활성화 함수
퍼셉트론에서는 활성화 함수로 계단 함수를 이용합니다. 활성화 함수를 계단 함수에서 다른 함수로 변경하는 것이 신경망의 세계로 나아가는 열쇠입니다.
2.1 시그모이드 함수
다음은 시그모이드 함수(sigmoid function)를 나타낸 식입니다.

신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고, 그 변환된 신호를 다음 뉴런에 전달합니다.
퍼셉트론과 신경망의 주된 차이는 이 활성화 함수 뿐입니다.
2.2 계단 함수 구현하기
계단 함수는 입력이 0을 넘으면 1을 출력하고, 그 외에는 0을 출력하는 함수입니다.
def step_function(x):
if x > 0:
return 1
else:
return 0
넘파이 배열을 이용해 계단 함수 구현하기
def step_function(x):
y = x > 0
return y.astype(np.int)
넘파이를 이용하여 두줄로 계단 함수를 구현할 수 있는 이유
넘파이 배열에 부등호 연산을 수행하면 배열의 원소 각각에 부등호 연산을 수행한 bool 배열이 생성됩니다.
import numpy as np
x = np.array([-1.0, 1.0, 2.0])
y = y > 0
print(y) # array([False, True, True], dtype=bool)
astype() 를 이용하여 배열의 자료형을 인수로 바꿔줍니다.
y = y.astype(np.int)
print(y) # array([0, 1, 1]) True는 1로, False는 0으로 변환됩니다.
2.3 계단 함수의 그래프
matplotlib 라이브러리를 사용하여 계단 함수를 그래프로 그려봅시다.
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x > 0, dtype=np.int) # 넘파이 배일여 0보다 클시에 1을 반환, 0보다 작으면 0을 반환합니다.
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # y축의 범위 지정
plt.show()
그래프에서 보면 계단 함수는 0을 경계로 출력이 0에서 1(또는 1에서 0)로 바뀝니다.
2.4 시그모이드 함수 구현하기
이어서 시그모이드 함수를 구현해봅시다.
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# np.exp(-x)는 exp(-x) 수식에 해당한다. 인수 x가 넘파이 배열이어도 올바른 결과가 출력됩니다.
# (넘파이의 브로드캐스트 기능)
시그모이드 함수를 그래프로 그려봅시다.
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # y축 범위 지정
plt.show()

2.5 시그모이드 함수와 계단 함수 비교

시그모이드 함수는 연속적인 실수가 흐릅니다. (이 매끈함이 신경망 학습에서 아주 중요한 역할을 합니다.)
계단 함수는 0혹은 1이 흐릅니다.
두 함수 모두 입력이 잘을 때의 출력은 0에 가깝고, 입력이 커지면 출력이 1에 가까워지는 구조입니다.
입력이 중요하면 큰 값을 출력하고 입력이 중요하지 않으면 작은 값을 출력합니다.
출력은 0에서 1사이, 비선형 함수라는 것도 둘의 공통점입니다.
2.6 비선형 함수
선형함수: 출력이 입력의 상수배만큼 변하는 함수입니다. 수식으로는 $f(x) = ax + b$이고, 이때 $a$와 $b$는 상수입니다.
비선형함수: 선형이 아닌 함수입니다. 직선 1개로는 그릴 수 없는 함수를 의미합니다.
신경망에서는 활성화 함수로 비선형 함수를 사용해야 합니다.
이유는 선형 함수를 이용하면 신경망의 층을 깊게하는 의미가 없어지기 때문입니다.
예를 들어 선형 함수인 $h(x) = cx$를 활성화 함수를 사용한 3층 네트워크를 이용한다면 식은 $y(x) = h(h(h(x)))$ 가 됩니다. 이 식은 $y(x) = c * c * c * x$ 처럼 곱셉을 세번 수행하지만, 실은 $y(x) = ax$와 똑같은 식이 된다. $a = c^{3}$와 같기 때문입니다.
따라서 층을 쌓은 이점을 얻고 싶다면 활성화 함수로는 반드시 비선형 함수를 사용해야 합니다.
2.7 ReLU 함수
최근에는 ReLU 함수를 주로 이용합니다.
ReLU는 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 0을 출력하는 함수입니다.

수식으로는 다음과 같이 나타낼 수 있습니다.

ReLu함수를 구현해봅시다.
def relu(x):
return np.maximum(0, x)
# 여기에는 넘파이의 maximum 함수를 사용했습다.
# maximum은 두 입력중 큰 값을 선택해 반환하는 함수입니다.3. 다차원 배열의 계산
넘파이의 다차원 배열을 사용한 계산 법을 숙달하면 신경망을 효율적으로 구현할 수 있습니다.
이번 내용은 넘파이의 다차원 배열 계산에 대해서 설명한 뒤 신경망을 구현해봅시다.
3.1 다차원 배열
다차원 배열은 숫자를 N차원으로 나열하는 것을 통틀어 의미합니다.
넘파이를 이용하여 다차원 배열을 작성해봅시다.
1차원 배열
import numpy as np
A = np.array([1, 2, 3, 4])
print(A) # [1,2,3,4]
np.ndim(A) # 1 배열의 차원 수를 의미합니다.
A.shape # (4,) 배열의 형상을 의미합니다. 1차원 배열이고 원소 4개로 구성, 튜플로 반환합니다.
# 2차원 배열일 떄는 (4, 3), 3차원 배열일 때는 (4, 3, 2)
A.shape[0] # 4
2차원 배열
B = np.array( [ [1, 2], [3, 4], [5, 6] ] )
print(B)
[ [1 2]
[3 4]
[5 6] ]
np.ndim(B) # 2 2차원을 의미합니다.
B.shape # (3, 2) 3행 2열을 의미하며 처음 차원에는 원소가 3개, 다음 차원에는 원소가 2개가 있다는 의미입니다.
2차원 배열은 행렬이라고 부르고 배열의 가로 방향을 행(row), 세로 방향을 열(column)이라고 합니다.
3.2 행렬의 내적(행렬 곱)
이어서 행렬(2차원 배열)의 내적을 구하는 방법을 알아봅시다.
2 X 2 행렬의 내적은 아래 그림처럼 계산합니다.

파이썬으로 행렬의 내적 구현하기
A = n[.arrat([ [1, 2], [3, 4] ])
A.shape # (2, 2) 행렬의 형태 2행 2열을 의미합니다.
B = np.array([ [5, 6], [7, 8] ])
B.shape # (2, 2)
np.dot(A, B) # 넘파이 .dot함수로 내적을 쉽게 구할 수 있습니다.
=> array([ [19, 22], [43, 50] ])
한가지 주의할 점은 np.dot(A ,B)와 np.dot(B, A)는 다른 값이 될 수 있습니다.
2 X 3 행렬과 3 X 2 행렬의 내적 구현하기
A = np.arrat([ [1, 2, 3], [4, 5, 6] ])
A.shape # (2, 3)
B = np.array([ [1, 2], [3, 4], [5, 6] ])
B.shape # (3, 2)
np.dot(A, B)
>> array([ [22, 28], [49, 64] ])다차원 배열을 곱하려면 두 행렬의 대응하는 차원의 원소 수를 일치시켜야 합니다.

3.3 신경망의 내적
넘파이 행렬을 이용하여 신경망을 구현해봅시다.
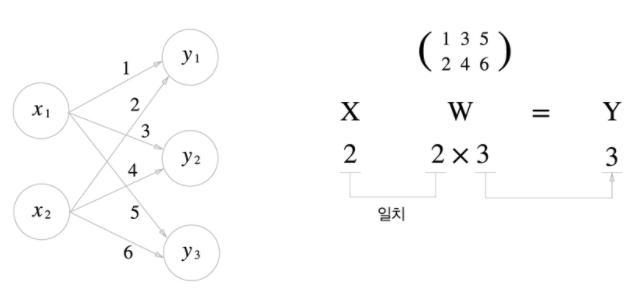
이 신경망은 편향과 활성화 함수를 생략하고 가중치만 갖습니다.
X와 W의 대응하는 차원의 원소수가 같아야 합니다.
X = np.array( [1, 2] )
X.shape # (2,)
W = np.array( [ [1, 3, 5], [2, 4, 6] ] )
print(W)
>>> [[1, 3, 5]
[2, 4, 6]]
W.shape # (2, 3)
Y = np.dot(X, W)
print(Y)
>>> [ 5, 11, 17 ]
4. 3층 신경망 구현하기
이번에는 3층 신경망에서 수행되는 입력부터 출력까지의 처리(순방향 처리)를 구현해봅시다.

위 그림의 3층 신경망은 입력층(0층) 2개, 첫 번째 은닉층(1층) 3개, 두 번째 은닉층(2층) 2개, 출력층(3층) 2개의 뉴런으로 구성됩니다.
4.1 표기법 설명
신경망 동작을 설명하기 위한 표기법을 알아 봅시다.

4.2 각 층의 신호 전달 구현하기
입력층에서 '1층의 첫 번째 뉴런'으로 가는 신호를 살펴봅시다.

편향을 뜻하는 뉴런이 추가되었다. 편향은 오른쪽 아래 인덱스가 하나밖에 없다는 사실을 주의해야 합니다.
그럼 지금까지 확인한 것을 반영하여 $a_{1}^{(1)}$을 수식으로 나타내보겠습니다.
$a_{1}^{(1)}$은 가중치를 곱한 신호 두 개와 편향을 합해서 다음과 같이 계산합니다.

여기서 행렬의 내적을 이용하면 1층의 '가중치 부분'을 다음 식처럼 간소화 할 수 있습니다.

이때 행렬 $A^{(1)}$, $X$, $B^{(1)}$, $W^{(1)}$은 각각 다음과 같습니다.

넘파이를 이용하여 위 식을 구현해보겠습니다. (가중치, 편향, 입력은 적당한 값으로 설정하였습니다.)
X = np.array( [1.0, 0.5] )
W1 = np.array( [0.1, 0.3, 0.5], [0.2, 0.4, 0.6] ] )
B1 = np.array( [0.1, 0.2, 0.3] )
W1.shape # (2, 3)
X.shape # (2,)
B1.shape # (3,)
A1 = np.dot(X, W1) + B1
이어서 1층의 활성화 함수에서의 처리를 살펴봅시다. 이 활성화 함수의 처리를 그림으로 나타내면 다음과 같이 됩니다.

그림과 같이 은닉층에서 가중치 합(가중 신호와 편향의 총합)을 $a$로 표기하고 활성화 함수 $h$()로 변환된 신호를 $z$로 표기합니다. 활성화 함수로 시그모이드 함수를 사용하기로 하겠습니다.
Z1 = sigmoid(A1)
print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.57444252. 0.66818777, 0.75026011]
이어서 1층에서 2층으로 가는 과정과 구현을 살펴보겠습니다.

W2 = np.array( [ [0.1, 0.4], [0.2, 0.5], [0.3, 0.6] ] )
B2 = np.array( [0.1, 0.2])
print(Z1.shape) # (3,)
print(W2.shape) # (3, 2)
print(B2.shape) # (2,)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)이처럼 넘파이 배열을 사용하면 층 사이의 신호 전달을 쉽게 구현할 수 있습니다.
마지막으로 2층에서 출력층으로의 신호 전달입니다.
은닉층과 다른점은 활성화 함수만 다릅니다.

출력층의 활성화 함수를 $\sigma$()로 표시하여 은닉층의 활성화 함수 $h$()와는 다름을 명시했습니다.
출력층 활성화 함수는 항등 함수를 이용합니다.
항등 함수는 입력을 그대로 출력하는 함수입니다.
def identity_function(x): # 출력층 활성화 함수는 함등함수를 이용했습니다.
return x
W3 = np.array( [ [0.1, 0.3], [0.2, 0.4] ] )
B3 = np.array( [0.1, 0.2] )
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) # 혹은 Y = A3
4.3 구현 정리
지금까지 구현을 정리해보도록 하겠습니다.
우선 순전파 처리만 구현했으며, 역전파 처리는 나중에 알아보겠습니다.
def init_network(): # 가중치와 편향을 초기화하고 이들을 딕셔너리 변수인 network에 저장합니다.
network = {}
network['W1'] = np.array( [ [0.1, 0.3, 0.5], [0.2, 0.4, 0.6] ] )
networt['b1'] = np.array( [0.1, 0.2, 0.3] )
network['W2'] = np.array( [ [0.1, 0.4]. [0.2, 0.5], [0.3, 0.6] ] )
network['b2'] = np.array( [0.1, 0.2] )
network['W3'] = np.array( [ [0.1, 0.3], [0.2, 0.4] ] )
network['b3'] = np.array( [0.1, 0.2] )
return network
def forward(network, x): # 입력 신호를 출력으로 변환하는 처리 과정을 구현합니다.
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = n[.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_fuction(a3) # identity_fuction은 위에서 정의한 출력층 항등 함수를 의미합니다.
return y
network = init_network()
x = np.array( [1.0, 0.5] )
y = forword(network, x)
print(y) # [0.31682708 0.69627909]
이로써 3층 신경망의 순전파 처리를 구현해보았습니다.
다음 포스팅에서는 출력층 설계와 MNIST 구현을 해보겠습니다. 감사합니다.
'수학 > 딥러닝 이론' 카테고리의 다른 글
| 03-3. 신경망 학습 (3) - 학습 알고리즘 구현 (1) | 2020.09.11 |
|---|---|
| 03-2. 신경망 학습 (2) - 기울기와 경사하강법 (0) | 2020.09.11 |
| 03-1. 신경망 학습 (1) - 손실 함수와 수치 미분 (0) | 2020.09.10 |
| 02-2. 신경망 (2) - 출력층 설계와 MNIST 구현 (6) | 2020.09.09 |
| 01. 퍼셉트론 - Perceptron (3) | 2020.09.06 |