딥러닝 공부방

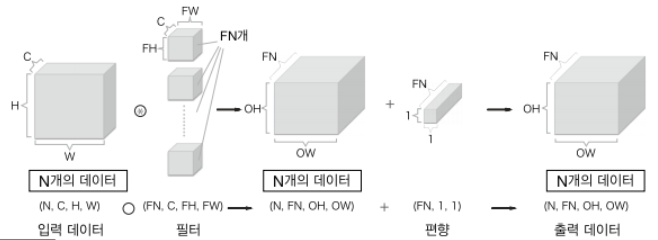
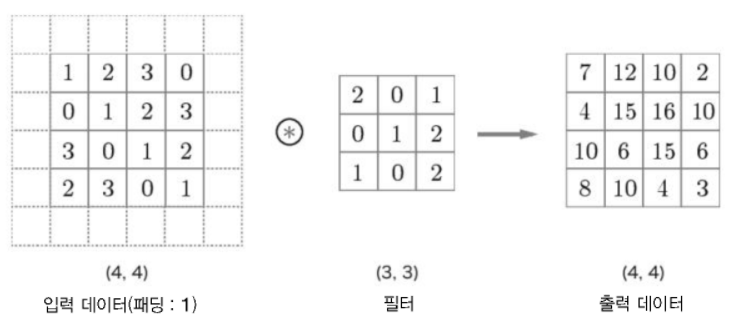
황선규 박사님의 , 패스트 캠퍼스 OpenCV 강의를 공부한 내용을 정리해 보았습니다. [파이썬 OpenCV] 영상의 기하학적 변환 - 전단 변환 - cv2.warpAffine 황선규 박사님의 , 패스트 캠퍼스 OpenCV 강의를 공부한 내용을 정리해 보았습니다. [파이썬 OpenCV] 영상의 기하학적 변환 - 이동 변환 - cv2.warpAffine 황선규 박사님의 , 패스트 캠퍼스 OpenCV 강의를 공 deep-learning-study.tistory.com 저번 포스팅에서 전단 변환에 대해 공부했습니다. 이번 포스팅에서는 크기 변환과 대칭 변환이 대해서 공부하도록 하겠습니다. 1. 크기 변환 - Scale transformation 영상의 크기를 원본 영상보다 크게 또는 작게 만드는 변환입니다. ..

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 두 모집단 비율 비교 독립표본을 통해 두 범주로 이루어진 두 모집단의 비율을 비교하는 방법을 알아보겠습니다. 비율 차에 대한 중심축량과 이를 바탕으로 한 구간추정방법을 알아보겠습니다. 1. 모집단 가정과 점추정, 중심축량 구하기 각각의 모집단은 동일한 두 범주 (S, F)로 나누어져 있다고 가정하겠습니다. 여기서 S는 성공, F는 실패입니다. 또 각각의 표본은 정규분포를 따른다고 가정하겠습니다. 관심문제를 설정하겠습니다. 4번이 통계적 성질은 가장 좋지만, 형태가 어려우므로 이 강의에서는 1번 비율차에 대해서 다뤘습니다. 두 모집단에서 베르누이 시행으로 표본을 추출했다고 가정하겠습니다. 모집단을 가정 했으므로 비율차에 대한 점..

사이토고키의 을 공부하고 정리해보았습니다. [딥러닝] 합성곱 신경망(CNN) - 3차원 데이터의 합성곱 연산 - 가중치와 편향 사이토고키의 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 을 공부하고 정리�� deep-learning-study.tistory.com 이전 포스팅에서는 3차원 데이터의 합성곱 연산에 대해서 공부했습니다. 이번에는 합성곱 신경망에서 배치 처리와 풀링 계층에 대해서 알아보겠습니다. 1. 배치 처리 신경망 처리에서는 입력 데이터를 한 덩어리로 묶어 배치로 처리했습니다. 완전연결 신경망을 구현하면서는 이 방식을 지원하여 처리 효율을 높이고, 미니배치 방식의 학습도 지원하도록 했습니다. 합성곱 연산도 마찬가지로..

사이토고키의 을 공부하고 정리해보았습니다. [딥러닝] 합성곱 신경망(CNN) - 합성곱 연산에서의 패딩과 스트라이드 사이토고키의 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 합성곱 신경망 - C deep-learning-study.tistory.com 이전 포스팅에서 합성곱 연산에서의 패딩과 스트라이드 기법을 공부했습니다. 이번에는 3차원 데이터의 합성곱 연산에 대해 공부하겠습니다. 3차원 데이터의 합성곱 연산 지금까지 2차원 형상을 다루는 합성곱 연산을 살펴봤습니다. 그러나 이미지만 해도 세로, 가로, 채널의 3차원 데이터입니다. 이번에는 채널까지 고려한 3차원 데이터를 다루는 합성곱 연산을 살펴보겠습니다. 3차원 데이터의 합..

사이토고키의 을 공부하고 정리해보았습니다. [딥러닝] 합성곱 신경망(CNN) - 합성곱 연산의 작동 방법 - 필터 사이토고키의 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 합성곱 신경망 - Convolutional neural network, CNN CNN은 � deep-learning-study.tistory.com 이전의 포스팅에서 합성곱 연산의 작동 방법과 필터의 개념에 대해 공부했습니다. 이번에는 합성곱 연산에서 자주 이용하는 기법인 패딩과 스트라이드에 대해 공부하겠습니다. 1. 패딩 - Padding 합성곱 연산을 수행하기 전에 입력 데이터 주변을 특정 값(예컨대 0)으로 채우기도 합니다. 이를 패딩이라 하며, 합성곱 연산에서 자주 이용하는 기법입니..

사이토고키의 을 공부하고 정리해보았습니다. [딥러닝] 합성곱 신경망(CNN) - 완전연결 계층(Affine 계층)의 문제점과 CNN의 특징 사이토고키의 을 공부하고 정리해보았습니다. 을 공부하고 정리해보았습니다. 합성곱 신경망 - Convolutional neural network, CNN CNN은 이미지 인식과 음성 인식 등 다양 deep-learning-study.tistory.com 이전 포스팅에서 완전연결 계층(Affine 계층)의 문제점과 CNN의 특징에 대해 알아보았습니다. 이번에는 합성곱 연산에 대해 알아보겠습니다. 합성곱 연산 합성곱 계층에서의 합성곱 연산을 처리합니다. 합성곱 연산은 이미지 처리에서 말하는 필터 연산에 해당합니다. 구체적인 예를 보겠습니다. 그림과 같이 합성곱 연산은 입력..

사이토고키의 을 공부하고 정리해보았습니다. [딥러닝] 합성곱 신경망(CNN) - CNN의 전체 구조 사이토고키의 을 공부하고 정리해보았습니다. 합성곱 신경망 - Convolutional neural network, CNN CNN은 이미지 인식과 음성 인식 등 다양한 곳에서 사용되는데, 특히 이�� deep-learning-study.tistory.com 이전 포스팅에서는 CNN의 전체 구조에 대해서 공부해봤습니다. 이번에는 완전연결 계층(Affine 계층)의 문제점에 대해 알아보겠습니다. 합성곱 계층 - Convolutional Layer CNN에서는 패딩(paddong), 스트라이드(stide) 등 CNN 고유의 용어가 등장합니다. 또, 각 계층 사이에는 3차원 데이터같이 입체적인 데이터가 흐른다는 점..

사이토고키의 을 공부하고 정리해보았습니다. 합성곱 신경망 - Convolutional neural network, CNN CNN은 이미지 인식과 음성 인식 등 다양한 곳에서 사용되는데, 특히 이미지 인식 분야에서 딥러닝을 활용한 기법은 거의 다 CNN을 기초로 합니다. CNN의 메커니즘을 공부하고 이를 파이썬으로 구현해보겠습니다. 전체 구조 CNN의 네트워크 구조를 살펴보며 전체 틀을 이해하도록 하겠습니다. CNN도 지금까지 본 신경망과 같이 레고 블록처럼 계층을 조합하여 만들 수 있습니다. 다만, 합성곱 계층(convolutional layer)과 풀링 계층(polling layer)이 새롭게 등장합니다. 합성곱 계층과 풀링 계층의 상세 내용은 나중에 공부하기로 하고, 여기서는 이 계층들을 어떻게 조합..

황선규 박사님의 , 패스트 캠퍼스 OpenCV 강의를 공부한 내용을 정리해 보았습니다. [파이썬 OpenCV] 영상의 기하학적 변환 - 이동 변환 - cv2.warpAffine 황선규 박사님의 , 패스트 캠퍼스 OpenCV 강의를 공부한 내용을 정리해 보았습니다. 영상의 기하학적 변환(geometric transformation)이란? 영상을 구성하는 픽셀의 배치 구조를 변경함으로써 전체 영상 deep-learning-study.tistory.com 이전 포스팅에서 영상의 이동 변환에 대해서 알아보았습니다. 이번에는 전단 변환에 대해 공부하겠습니다. 영상의 전단 변환 - Shear transformation 영상의 전단 변환은 층 밀림 변환이라고도 합니다. 이동을 하는데 모든 픽셀들이 동일하게 이동하는 ..

황선규 박사님의 , 패스트 캠퍼스 OpenCV 강의를 공부한 내용을 정리해 보았습니다. 영상의 기하학적 변환(geometric transformation)이란? 영상을 구성하는 픽셀의 배치 구조를 변경함으로써 전체 영상의 모양을 바꾸는 작업입니다. 영상의 모양 자체를 변환하고 좌표에 대한 개념이 필요합니다. 기하학적 변환이 필요한 이유 1. 입력 영상 크기가 제한되어 있어 영상 크기를 축소해야 하는 경우. 2. 객체가 영상의 정중앙에 있어야 하는 경우. 3. 회전이 되어 있는 영상을 똑바로 보정 이 외에도 여러가지 상황에서 영상의 기하학적 변환이 필요합니다. 1. 영상의 이동 변환 - Translation transformation 이동 변환은 shift라는 용어도 많이 씁니다. 가로 또는 세로 방향으로..