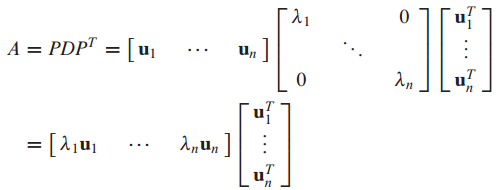딥러닝 공부방

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다. 대칭 행렬의 대각화는 선형대수학의 꽃인 SVD를 유도하기 위해 필요합니다. 대칭 행렬이 무엇이고 대칭 행렬을 대각화할때 나타나는 새로운 특성을 알아보도록 하겠습니다. 대칭 행렬(Symetric Matrix) 대칭 행렬은 행렬 A가 정사각 행렬(square matrix)이고, $A^T = A$를 만족하는 행렬입니다. 1) A가 정사각 행렬(square matrix) 2) $A^T = A$ 위 두 가지 조건을 만족하면 대칭 행렬입니다. 대칭 행렬의 예시를 살펴보겠습니다. 대칭 행렬이 아닌 경우입니다. 대각화(Diagonalization) 대칭 행렬의 대각화를 살펴보기 전에 이전에..

이번 포스팅에서 공부할 내용은 대각화(Diagonalization)입니다. 1. 대각화(Diagonalization) 정사각행렬(square matrix) A가 대각 행렬(diagonal matrix)와 유사(similar)하면 A를 대각화가능(diagonalizable)하다고 합니다. 즉, A = PD$P^{-1}$ 일 때 A가 diagobalizable이라고 합니다. 예시 문제 1 diagonal matrix의 squre은 diagonal term의 squre입니다. 만약 A가 D와 similar하면 $A^k$를 쉽게 계산할 수 있습니다. 예시 문제 2 A가 diagonalizable할 때, $A^k$를 구하는 문제입니다. 2. 이론 4. 대각화 이론 - Theorem 4. The Diagonaliz..