이번 포스팅에서 공부할 내용은 대각화(Diagonalization)입니다.
1. 대각화(Diagonalization)
정사각행렬(square matrix) A가 대각 행렬(diagonal matrix)와 유사(similar)하면 A를 대각화가능(diagonalizable)하다고 합니다.
즉, A = PD$P^{-1}$ 일 때 A가 diagobalizable이라고 합니다.
예시 문제 1
diagonal matrix의 squre은 diagonal term의 squre입니다.




만약 A가 D와 similar하면 $A^k$를 쉽게 계산할 수 있습니다.
예시 문제 2
A가 diagonalizable할 때, $A^k$를 구하는 문제입니다.

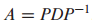
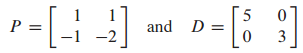
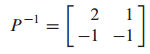
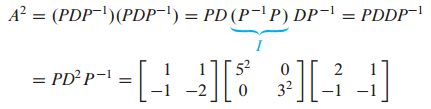

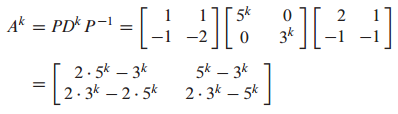
2. 이론 4. 대각화 이론 - Theorem 4. The Diagonalization Theorem

nxn 행렬 A가 diagobalizable이면 A는 n개의 linearly independent eigenvector를 갖고 있습니다.
즉, D가 diagonal matrix이고 A = PD$P^{-1}$이면, P의 column은 A의 n 개의 linearly independent eigenvector로 이루어져 있습니다.
이 경우에 D의 diagobal entries는 P를 구성하는 eigenvector 각각에 대한 A의 eigenvalues 입니다.
증명
P가 $v_1, ... ,v_n$로 이루어진 nxn 행렬이고 D가 eigenvalues를 diagonal entries로 갖고 있는 diagonal matrix이면 다음과 같습니다.




P가 invertible이므로 A = PD$P^{-1}$이 성립하게 됩니다.
주의할 점으로 eigenvalues는 distinct일 필요가 없습니다.
중복되어도 n 개의 eigenvector가 나올 수 있습니다.
3. 행렬 대각화하기 - Diagonalizing Matrices
행렬을 diagonalization 하는 방법을 알아보겠습니다.

첫 번째로 행렬의 eigenvalues를 찾아야 합니다.
eigenvalues는 characteristic equation을 이용해서 찾을 수 있습니다.


두 번째로 행렬의 eigenvector을 찾아야 합니다.
이는 $\lambda$에 대한 basis를 의미합니다.
eigenvector를 찾기 위해서 (A-$\lambda$)x = 0의 general solution을 찾고 eigenvector를 찾고 eigenspace를 찾아서 basis를 찾습니다.
eigenvector를 찾았으면 n개인지 확인해야 합니다.
eigenvector가 n보다 작으면 diagonalization이 불가능합니다.
eigenvector로 P를 구성합니다.
P는 column이 각각의 eigenvector로 구성된 행렬입니다.

D는 diagonal entries가 eigenvalues인 diagonal matrix 입니다.
위에서 구한 eigenvalues로 D 행렬을 구성하면 됩니다.
주의할 점으로는 P의 eigenvector에 해당되는 eigenvalue를 diagonal entry로 두어야 합니다.
예시 문제 1
다음의 행렬을 diagonalize하는 문제입니다.

(1) det(A-$\lambda$I)=0을 이용해서 A의 eigenvalue를 찾습니다.

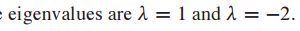
(2) A의 eigenspace의 basis를 찾습니다.
eigenspace의 basis는 (A-$\lambda$I)x=0의 general solution을 구하여 찾을 수 있습니다.

각각의 vector가 independent set인지 확인합니다.
또한 vector의 개수가 n개인지 확인합니다.
만약 n보다 적으면 diagonalization이 불가능합니다.
(3) eigenvector를 이용해서 행렬 P를 구성합니다.

(4) eigenvalue를 이용해서 행렬 D를 구성합니다.

4. 이론 5. - Theorem 5

n개의 eigenvalue가 모두 distinct이면 diagonalizable합니다.
n개의 distinct eigenvalue를 갖고 있으면 그 matrix는 n개의 independent eigenvector를 갖는다는 의미입니다.
따라서 diagonalizable입니다.
예시 문제
주어진 행렬이 diagonalizable한지 확인하는 문제입니다.

이 문제는 쉽습니다.
triangular matrix이므로 diagonal term이 eigenvalue입니다.
각각의 eigenvalue가 distinct이므로 3개의 eigenvector가 존재하게 됩니다.
따라서 diagonalizable 합니다.
5. 이론 6- Theorem 6

주어진 nxn 행렬 A가 p개의 eigenvalues를 지니고 있을 때의 이론입니다.
a. eigenvalue의 multiplicity가 3이면 그에 해당하는 eigenspace의 dim은 3이하입니다.
b. eigenvalue에 해당하는 eigenspace의 dim은 eigenvalue의 multiplicity 이하이고, 별개의 eigenspace의 dim의 합이 n가 동일하면 diagonalizable입니다.
예를 들어 eigenvalue의 multiplicity가 1,2로 주어졌으면 각각의 eigen value에 대한 eigen space의 dim은 1,2이어야만 matrix가 diagonalizable 합니다.
예시 문제
OX 문제입니다.
(1) A가 n개의 eigenvector를 지니고 있으면 diagonalizable이다.
정답 : x입니다. eigenvector가 linearly independent 조건이 필요합니다.
(2) A가 diagonalizable이면 A는 n개의 distinct eigenvalue를 갖고 있다.
정답 : x입니다. eigenvalue는 중복될 수 있습니다. 중복된 수 만큼 multiplicity로 표현합니다.
(3) D가 diagonal이고 AP=PD이면 P의 nonzero column은 A의 eigenvector이다.
정답 : o입니다.
(4) A가 invertible이면 A는 diagonalizable이다.
정답 : x입니다. invertible의 의미는 A의 모든 column이 linearly independent를 의미합니다. diagonalizable은 A가 n개의 independent eigenvector를 갖고 있다는 의미입니다.