이번 포스팅에서 공부할 내용은 다음과 같습니다.
크라메이 법칙 - Cramer's Rule
역행렬 공식 - Inverse formula
면적과 부피에서 행렬식 - Determinants as area and volumn
선형 변환 - Linear transformation
1. 크라메이 법칙 - Cramer's Rule
Cramer's Rule을 사용하기 위해서는 새로운 정의가 필요합니다.

A의 i th column을 b로 치환한 것을 $A_i(b)$로 표현하겠습니다.
2. 이론 7. 크라메이 법칙 - Theorem 7. Cramer's Rule
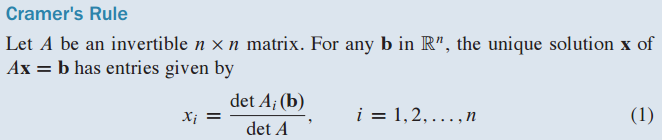
A가 n x n 크기의 invertible 행렬일 때 Ax=b의 해는 다음과 같이 구할 수 있습니다.

$A_i(b)$는 A행렬의 i th culumn을 b로 치환한 것입니다.
크라메이 법칙은 matrix size가 커질수록 비효율적이므로 유용한 것은 아닙니다.
증명
A의 column을 $a_1, ... , a_n$으로 나타내고 항등 행렬인 I 의 column을 $e_1, ... , e_n$으로 나타내겠습니다.
Ax=b를 행렬 곱으로 나타내면 다음과 같습니다.

이때, 이전 포스팅에서 배운 multiplicative property of determinant에 의해 다음과 같이 표기할 수 있습니다.

det$I_i$(x)를 cofactor expansion을 해보면 $x_i$가 됩니다.
따라서 다음과 같이 표현됩니다.


예시 문제
Cramer's rule을 사용해서 주어진 방정식을 푸는 문제입니다.


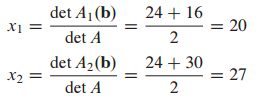
3. $A^{-1}$에 대한 공식 - A Formula for $A^{-1}$
Cramer's Rule을 사용해서 $A^{-1}$를 명시적인 상태로 표현할 수 있습니다.
$A^{-1}$의 j th column이 vector x 일때 다음을 만족합니다.

$e_j$는 항등 함수 i의 j th column이고 x는 $A^{-1}$의 j th column이므로 $x_i$는 $A^{-1}$의 (i,j) entry입니다.
따라서 Cramer's rule에 의해 다음이 성립합니다.

$A_{ji}$가 row j, column i를 제거한 A의 부분행렬을 나타내므로 ,det$A_i(e_j)$는 cofactor expansion으로 다음과 같이 표현할 수 있습니다.

$C_{ji}$는 A의 cofactor이므로 $A^{-1}$의 (i,j) entry는 $C_{ji}를 det A로 나눈 것과 동일합니다.
따라서 $A^{-1}$를 다음과 같이 표현할 수 있습니다.

cofactor의 matrix를 수반 행렬(adjugate or adjoint or classical matrix)라고 합니다.
그리고 adj A로 간단히 표현합니다.
4. 이론 8. 역 공식 - Theorem 8. An Inverse Formula

$A^{-1}$를 adjugate matrix로 표현할 수 있습니다.
이 방식으로 $A^{-1}$를 구하는 것은 굉장히 비효율 적입니다.
예시 문제
행렬 A의 역행렬을 찾는 문제입니다.



adj A와 A를 내적하면 det A를 구할 수 있습니다.


5. 면적 또는 부피로서의 행렬식 - Determinants as Area or Volumn
$R^2$와 $R^3$에 존재하는 어떤 matrix의 det는 면적과 부피에 밀접한 관련이 있습니다.


column가 (a,0), (0,d)인 matrix의 determinant는 면적을 의미합니다.
matrix의 determinant가 a x d 이기 때문입니다.

column이 (a,0, 0), (0, b, 0), (0, 0, c)인 matrix도 동일합니다.
determinant가 a x b x c이기 때문입니다.
6. 이론 9. - Theorem 9.
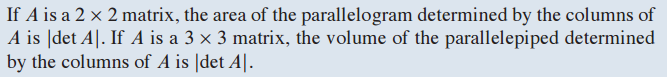
2 x 2 행렬의 det는 면적이고, 3 x 3 행렬의 det는 부피입니다.
증명

평행사변형으로 표현되는 matrix를 row reduction 연산을 통해 echelon form으로 변환하면 도형이 x,y 축에 붙도록 변형됩니다.
echelon form과 pivot값들은 여러가지이지만 pivot의 곱은 항상 동일하므로 det이 면적을 의미하게 됩니다.
예시 문제
주어진 행렬의 면적을 구하는 문제입니다.


7. 이론 10. 선형 변환 - Theorem 10. Linear Transformation

A는 linear transformation의 standard matrix를 의미합니다.
$R^2$ 공간에 존재하는 S를 A 행렬로 linear transformation을 한 T(S)의 면적은 det A x S의 면적과 동일합니다.
$R^3$ 공간에 존재하는 S를 A 행렬로 linear transformation을 한 T(S)의 부피는 det A x S의 부피와 동일합니다.

이론 10은 평행사변형이 아니더라도 임의의 도형에 적용할 수 있습니다.
예시 문제
주어진 타원 방정식의 면적을 구하는 문제입니다.


linear transformation의 standard matrix인 A는 다음과 같습니다.

따라서 원래 원의 면적인 $\pi$와 det A를 곱하면 ab$\pi$가 됩니다.

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 4.2 특성 방정식 - The Characteristic Equation - 유사도(similar), similar transformation (0) | 2020.12.05 |
|---|---|
| [선형대수학] 4.1 고유벡터와 고유값 - Eigenvectors and eigenvalue (0) | 2020.11.30 |
| [선형대수학] 3.2 행렬식의 성질 - Properties of Determinants (0) | 2020.11.20 |
| [선형대수학] 3.1 행렬식 개요 - Introduction to Determinants - 행렬식, 여인수, 여인수 전개 (0) | 2020.11.20 |
| [선형대수학] 2.7 차원과 계수 - Dimension and Rank - 좌표계와 좌표벡터, 차원, 계수 (1) | 2020.11.15 |