이번 포스팅에서 알아볼 내용은 차원과 계수(Dimension and Rank)입니다.
좌표계와 좌표벡터 - Coordinate system and coordinate vector
차원 - Dimension
계수 - Rank
에 대해 공부하고 정리해보았습니다.
1. 부분공간에서의 기저 - Basis for a Subpace
차원과 계수, 좌표계를 알아보기 전에 기저(basis)를 복습하겠습니다.
basis는 independent set으로 표현되는 최소한의 vector를 의미합니다.
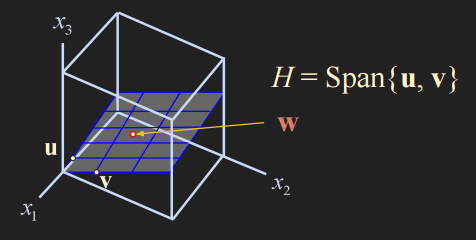
u와 v는 independent 관계이며 Span{u,v}는 $R^3$공간에서 2차원 평면을 표현합니다.
Span{u,v}뿐 아니라 Span{u,w}와 Span{v,w}도 basis가 될 수 있습니다.
u와 w, v와 w는 independent이기 때문입니다.
basis는 특정 구속조건이 있지 않는한 유일하지 않습니다.
다양한 basis가 존재할 수 있으며 특정 구속 조건이 있는 경우는 standard basis라고 합니다.
각각의 축에 해당하는 단일 크기 vector로 이뤄진 것이 standard basis 입니다.
2. 좌표계 - Coordinate Syetems
부분공간 H에 존재하는 각각의 vector는 basis vector의 linear combination으로 표현할 수 있습니다.
H 부분공간에서 basis B={$b_1, ... ,b_p$}를 가정하겠습니다.
H에 있는 vector 는 다음과 같이 생성될 수 있습니다.

두 식을 빼면 다음과 같이 됩니다.

B가 linearly independent이므로 각각의 weights는 0이 되어야합니다.
trivial solution만 존재하므로 scalar 값은 0밖에 없기 때문입니다.
즉, $c_j = d_j$가 됩니다.
basis가 주어졌을 때 특정 X vector를 표현하는 weight는 유일합니다.
$R^2$ space x,y 좌표계를 standard basis로 표현하면 [1,0], [0,1]이 됩니다.
[1,1]를 표현하는 방법은 1가지 방법밖에 없습니다.
3. 좌표와 좌표 벡터 - Coordinates and Coordinate Vector

x를 linear combination으로 표현했을 때 각각의 cordinate를 vector로 표현한 것이 cordinate vector입니다.
일반 좌표계가 아닌 basis이기 때문에 linearly independent입니다.
예시 문제
$v_1, v_2, x$가 주어졌을 때 x를 B에 대한 coordinate vector로 표현하는 문제입니다
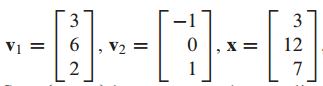

$v_1, v_2$는 basis 이므로 x를 $v_1, v_2$의 linear combination으로 표현할 수 있습니다.

위 방정식을 Row operation으로 $c_1, c_2$를 구할 수 있습니다.
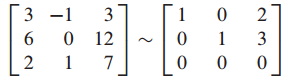
$c_1 = 2, c_2 = 3$ 이므로 x의 coordinate vector은 다음과 같이 됩니다.
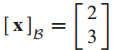
이를 시각화하면 다음과 같이 표현됩니다.

여기서 H는 $R^2$에 동형관계(isomorphic)에 있다고 합니다.
basis vector은 $R^3$에 존재하지만 subspace H가 마치 $R^2$ space에 존재하는 것처럼 동작하기 때문입니다.
실제로 각각의 vector는 $R^3$ space에 있지만 H는 $R^2$ space에서 동작하므로 isomorphic하다고 합니다.
또 transpormation은 one-to-one입니다.

basis set은 independent augmented matrix로 표현했을 때 row reduction을 진행하면 column 개수 만큼 pivot이 존재합니다.
이는 임의의 b가 존재할 때 해가 없거나 하나밖에 없음을 의미하므로 one-to-one 입니다.
4. 차원 - Dimension
basis의 차원이 정해질 수 있습니다.

dim H로 나타내는 nonzero subspace H의 dimension은 H의 basis에 존재하는 vector의 개수입니다.
zero subspace {0}의 dimension은 0 입니다.
zero vector set은 dependent이므로 basis가 정의가 안됩니다.
따라서 0 dimension이 됩니다.
3차원에서 origin(0,0)을 통과하는 평면은 2차원 입니다.
3차원에서 origine을 지나는 line은 1차원 입니다.
5. 계수 - Rank

matrix A의 rank는 A의 column space의 dimension을 의미합니다.
column space의 basis vector가 몇개 존재하는지 알면 그것이 dimension이 됩니다.
예시 문제
주어진 행렬의 계수를 구해라

A를 row reduction을 통해 echelon form으로 변환하고 pivot column을 찾습니다.

pivot column 위치의 A의 column이 A의 basis입니다.
pivot column이 3개 존재하므로 rank A는 3입니다.
추가적으로 null space의 dimension도 구할 수 있습니다.
free variable이 $x_3, x_5$ 2개 이므로 dim Nul A = 2 입니다.
Null space의 dimension은 free variable의 개수와 같습니다.
6. 이론 13. 계수 이론 - Theorem 13. The Rank Theorem
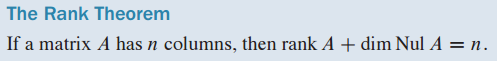
matrix A가 n개 column를 갖고 있을 때 rank A + dim Nul A = n 입니다.
rank A는 basic variable 개수, dim Nul A는 free variable 개수를 의미합니다.
7. 이론 14. 기저 이론 - Theorem 14. The Basis Theorem

H는 $R^n$의 p-차원 부분공간입니다.
H에서 p개의 linearly independent set은 H에 대한 basis 입니다.
p개의 vector가 H를 span하고 있으면 H의 basis가 됩니다.

p개 vector가 linearly dependent이면 A에서 pivot의 개수는 p보다 적습니다.
따라서 H에 존재하는 b는 Col A에 존재하지 않습니다.
pivot이 p개 보다 적으므로 zero row가 생기기 때문입니다.
Col A는 linear combination을 의미합니다.
만약 dependent set인 Col A에 b가 만족한다면 Col A는 H를 span하지 못합니다.
H가 2개의 linearly dependent vector로 이루어져 있을 때 subspace H안에 존재하지만 H를 span하지는 않습니다.
H를 span하려면 linearly independent가 되어야 하기 때문입니다.
8. 추가된 역행렬 이론 - The Invertible Matrix Theorem

기존의 역행렬 이론에서 추가되는 이론입니다.
9. 예시 문제
$v_1, v_2, v_3$에 의해 span하는 $R^3$ space의 subspace H의 dimension을 결정해라

첫번째로 H의 basis를 찾아야 합니다.
basis는 independent set을 의미하므로 echelon form으로 변환 후 pivot column 개수를 파악하면 됩니다.

pivot이 2개 이므로 dim A = 1, dim Nul A = 1입니다.

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
