이번 포스팅에서는 $R^n$ 공간에서의 부분공간(Subspaces)과 기저 대해 공부하겠습니다.
공부할 내용은 다음과 같습니다.
$R^n$ 공간에서의 부분공간 - Subspace of $R^n$
열 공간 - column space
영 공간 - null space
부분공간에서의 기저 - basis for subspace
1. $R^n$ 공간에서의 부분공간 - Subspace of $R^n$

부분 공간(subspace)를 H로 표현합니다.
H가 위 세 가지 조건에 부합하면 부분 공간이라고 합니다.
a. zero vector가 H set에 존재해야 합니다.
b. H에 있는 임의의 벡터 u와 v를 더한 u + v이 H안에 있어야 합니다.
c. H에 있는 임의의 벡터 u에 스칼라 c와 곱한 값 cu이 H안에 있어야 합니다.
단어로 표현하자면, 부분공간(subspace)은 스칼라 곱(scalar multiplication)과 덧셈(addition)에 닫혀(closed)있어야한다고 표현합니다.
또, $R^n$공간에서 zero vectors를 zero subspace라고 부릅니다.
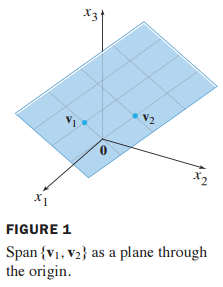
위 그림처럼 Span{$v_1, v_2$}는 원점(origin)을 지나는 평면인 $R^3$ 공간의 subspace가 됩니다.
2. 부분공간 예시문제 1

이는 H가 $R^n$의 부분공간(subspace)임을 묻는 문제입니다.
0$v_1$ + 0$v_2$ = 0 을 만족하므로 a 조건에 부합합니다.

덧셈이 성립하므로 b 조건도 부합합니다.

스칼라 곱도 성립하므로 c 조건도 부합합니다.
따라서 $R^n$공간에 있는 $v_1, ... ,v_p$가 주어졌을 때 Span{$v_1, ... ,v_p$}는 $R^n$의 부분공간입니다.
3. 부분공간 예시문제 2
직선 L이 원점을 통과하지 않으면 부분공간이 아닙니다.
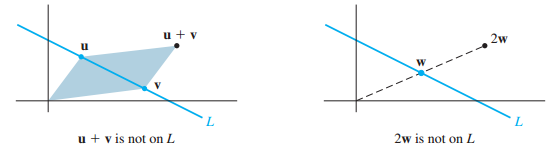
$R^2$ 공간에서 직선 L은 원점(0,0)을 지나지 않습니다.
이는 L이 zero vector을 포함할 수 없다는 것을 의미합니다.
또한 임의의 벡터 u와 v를 선택했을 때 덧셈은 L에 존재하지 않으며
스칼라 곱(scalar multiplication)도 직선 L에 존재하지 않습니다.
따라서 직선 L은 덧셈과 스칼라 곱에 닫혀있지 않게 됩니다.
직선 L은 subspace가 아닙니다.
4. 열 공간 - Column Space
열 공간(Column space)도 부분공간(subspace)입니다.

열 공간을 Col A라고 표현합니다.
열 공간은 A의 열들의 모든 선형결합을 의미합니다.
$R^m$공간에서 A = [$a_1, ... ,a_n$]으로 주어졌을 때 Col A = Span{$a_1, ..., a_n$}입니다.
즉, A의 열들을 Span한 것이 열 공간(column space)이며 $R^m$의 부분공간입니다.
5. 열 공간 A에 b가 존재하는가? - Is b in Col A?
이는 Ax=b가 해가 있는지(consistent)를 묻는 질문입니다.
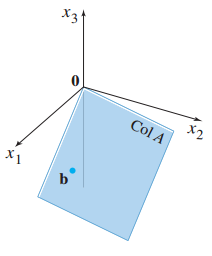
예시 문제를 살펴보도록 하겠습니다.
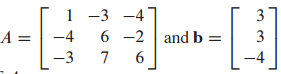
A와 b가 다음과 같이 주어졌을 때 Ax=b의 해가 존재하는지 확인해보겠습니다.
사다리 꼴(echelon from)으로 만들기 위해 첨가 행렬(augmented matrix)로 만들고 행 줄임(row reduction)을 진행하겠습니다.

pivot position이 2개이고 x3은 자유 변수(free variable)인 것을 확인했습니다.
이는 해가 무수히 많게 되므로 consistent 합니다.
결국 b는 A의 열 공간(column space)에 존재합니다.
6. 영 공간 - null space

행렬 A의 영 공간(null space)은 제차 방정식(homogeneous equation) Ax=0의 모든 해의 집합을 의미합니다.
이를 Nul A로 표현합니다.
Is u in Nul A? 의 질문은 Au = 0을 만족하는지 묻는 질문입니다.
7. 이론 12 - Theorem 12

m x n 행렬 A의 영 공간(null space)은 $R^n$ 공간의 부분공간입니다.
동일하게, n 개의 미지수를 갖고 있는 m개의 제차 방정식의 Ax=0의 모든 해의 집합은 $R^n$ 공간의 부분공간입니다.
증명
부분 공간의 3가지 조건에 부합하는지 확인해보겠습니다.
제차 방정식은 A0=0을 만족하므로 a 조건에 해당합니다.
덧셈도 만족하므로 b조건에 해당합니다.

스칼라곱도 만족하므로 c조건에 해당합니다.

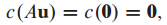
따라서 영 공간은 3가지 부분공간 조건에 부합하므로 부분공간이라고 할 수 있습니다.
8. 부분공간에서 기저 - Basis for a Subspace

$R^n$ 공간의 부분공간 H에 대한 기저(basis)는 H를 span하는 선형 독립 집합(linearly independent set)입니다.
9. $R^n$ 공간에서 표준 기저 - Standard Basis for $R^n$
표준 기저(standard basis)는 n x n 항등 행렬(identity matrix)에서 각각의 column을 갖고 온것입니다.

$e_1, ... ,e_n$ 집합을 $R^n$ 공간에서의 표준 기저(standard basis)라고 합니다.
항등 행렬의 열 집합이므로 선형 독립 집합입니다.

10. 기저를 찾는 예제 문제
예제 문제를 살펴보도록 하겠습니다.
(1) 행렬의 영 공간에 대한 기저를 찾아라 - Find a basis for the null space of the matrix

null space에서의 basis를 찾는 문제이므로 Ax=0 의 solution을 구합니다.

pivot position을 통해 $x_2, x_4, x_5$는 free variable이고 $x_1, x_3$은 basic variable임을 확인할 수 있습니다.
이를 general solution으로 표현하면 다음과 같습니다.

$x_2u + x_4v + x_5w$ = 0 을 풀면 $x_2, x_4, x_5$가 free variable이므로 trivial solution만 존재합니다.
이는 {u,v,w}가 linearly independent임을 의미합니다.
따라서 {u,v,w}가 null space에서의 basis입니다.
Homogeneous equation의 general solution은 Null space의 basis vector의 linear combination으로 표현됩니다.
(2) 열 공간에대한 기저를 찾아라 - Find a basis for the column space of the following matrix
column space는 행렬의 모든 column을 span한 것을 의미합니다.
문제에서 묻는 것은 최소한의 linearly independent set을 찾고자 하는 것입니다.
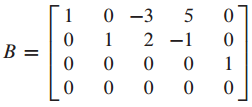
reduced echelon form으로 변환하면 pivot column을 찾을 수 있습니다.
pivot column 간 linearly independent가 성립하므로 {$b_1, b_2, b_5$}가 Col B를 span하고 basis 입니다.
pivot column이 아닌 column은 pivot column으로 표현이 가능합니다.
reduced echelon form이므로 각각의 column vector는 identity matrix에 있는 column vector의 일부입니다.
따라서 $b_1, b_2, b_5$는 linearly independent이고 나머지 $b_2, b_4$는 $b_1, b_2, b_5$의 set으로 표현됩니다.
(3) 열 공간에서 기저를 찾아라 - Find a basis for the column space of the following matrix

column space에서 pivot column을 파악하고 basis를 찾기 위해 row reduction을 통해 echelon form으로 만들어야 합니다.
여기서 중요한 것은 row operation(행 연산)은 행렬의 열들의 선형 종속 관계에 영향을 주지 않습니다.
echelon form으로 만들면 $a_1, a_2, a_5$이 pivot column인 것과 이 columns은 linearly independent인 것을 확인할 수 있습니다.
따라서 A의 column space의 basis는 $a_1, a_2, a_5$ 이며 {$a_1, a_2, a_5$} spans Col A 입니다.
주의할 점은 echelon form의 pivot column이 basis가 아니라 원래 형태 행렬의 pivot column이 basis 입니다.
ColA와 ColB는 다릅니다.
모든 row가 pivot을 갖고 있는 경우만 ColA = ColB가 성립하며 이는 subspace가 space 전체를 의미합니다.
11. 이론 13 - Theorem 13

행렬 A의 pivot columns는 A의 column space의 basis입니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
