이번 포스팅에서는 분할 행렬(Partitioned matrix) or 블록 행렬(Block matrix)에 대해 알아보겠습니다.
분할 행렬 or 블록 행렬 - Partitioned Matrix of Block Matrix
덧셈과 스칼라 곱 - Addition and Scalar Multiplication
분할 행렬의 곱 - Multiplication of Partitioned Matrix
AB의 열-행 확장 - Column-row expansion of AB
분할 행렬의 역행렬 - Inverse of partitioned matrix
1. 분할 행렬 or 블록 행렬 - Partitioned Matrix or Block Matrix
matrix가 주어졌을 때 임의로 row와 column을 나눕니다.
이를 submatrix로 표현한 것을 분할 행렬(partitioned matrix) 또는 블록 행렬(block matrix)라고 합니다.
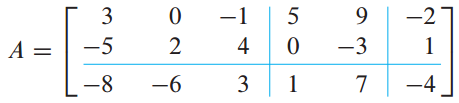
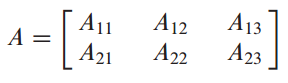

2. 덧셈과 스칼라 곱 - Addition and Scalar Multiplication
같은 크기(size)이고 같은 방법으로 분할 되었으면 덧셈을 할 수 있습니다.

스칼라 곱 rA은 각각 block에 r scalar multiplication을 적용하면 됩니다.
3. 분할 행렬의 곱 - Multiplication of Partitioned Matrix
분할 행렬(Partitioned matrix) A와 B가 다음과 같이 주어졌을 때

분할 행렬의 곱(Multiplication of partitioned matrix)는 다음과 같이 구할 수 있습니다.
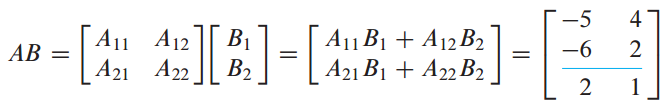
각각의 block을 단일 entry로 다뤄서 기존의 matrix multiplication을 이용하면 됩니다.

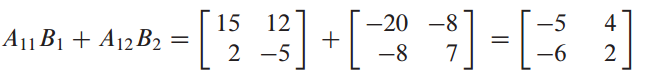
4. 이론 10. AB의 열-행 확장 - Column-Row Expansion of AB

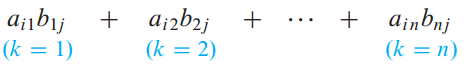
m X n 분할 행렬 A와 n X p 분할 행렬 B를 곱하면 m X p 행렬이 만들어집니다.
5. 분할 행렬의 역행렬 - Inverses of Partitioned Matrix

A matrix의 form이 block upper triangular로 주어지고 $A_{11}$은 p x p, $A_{22}$는 q x q이고 A가 invertible이라고 가정할 때 $A^{-1}$를 찾아보겠습니다.

여기서 B는 A의 역행렬 입니다.
Multiplication을 적용하면 4개의 식이 도출됩니다.
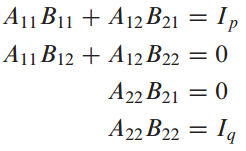
위 식을 이용해서 $A^{-1}$를 찾을 수 있습니다.

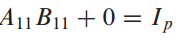


$B_{11}. B_{12}, B_{21}. B_{22}$를 구했으므로 B 행렬(A의 역행렬)을 표현할 수 있습니다.
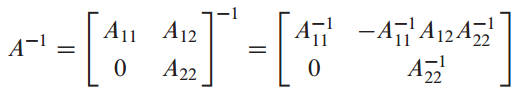
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
