이번 포스팅에서는 역행렬에 대해 알아보겠습니다.
역행렬이 존재하는 행렬 - Invertible Matrix
2x2 행렬에서의 결정자 (ad - bc) - determinant
기본 행렬 - Elementary matrix
$A^{-1}$를 찾는 알고리즘 - Algorithm for Finding $A^{-1}$
1. 숫자의 승수 역수 - Multiplicative Inverse of a Number
역행렬을 알아보기 전에 숫자의 승수 역수(multiplicative inverse of a number)를 살펴보겠습니다.
5의 역수는 1/5 입니다.

2. 역행렬이 존재하는 행렬 - Invertible Matrix
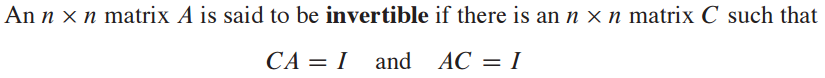
invertible의 첫번째 조건은 row와 column의 size가 동일해야 합니다.
또한 AC = I 인 C 행렬이 있어야 하며 C는 유일(unique)합니다.
C대신 $A^{-1}$로 표기합니다.

matrix가 not invertible이면 singular matrix(해가 존재하지 않는 행렬) 입니다.
invertible이면 nonsingular matrix(해가 존재)입니다.
3. 이론 4 - Theorem 4

A가 2x2 행렬일 때 ad-bc != 0이면 A는 invertible 합니다.
ad-bc = 0이면 not invertible 입니다.
여기서 ad-bc는 pivot position이 2개 있을 조건을 의미하며 determinant(결정자)라고 부릅니다.
어떤 matrix가 invertible을 판단할 때 determinant가 0인지 아닌지를 확인하면 됩니다.


4. 이론 5 - Theorem 5
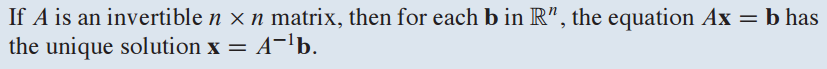
A가 invertible n X n matrix이면 $R^n$ 공간에 있는 b에 대한 방적식 Ax=b는 유일한 해(x=$A^{-1}$b)를 갖습니다.
증명


예시 문제
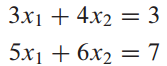

이처럼 A의 inverse를 이용하면 쉽게 solution을 구할 수 있습니다.
5. 이론 6 - Theorem 6
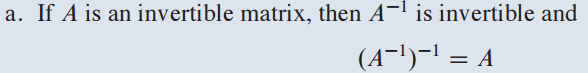
A가 invertible matrix이면 $A^{-1}$도 invertible 입니다.

$(AB)^{-1}$은 $B^{-1}A^{-1}$와 동일합니다.
주의할 점은 순서가 뒤바뀌어 B가 먼저 나온다는 것입니다.
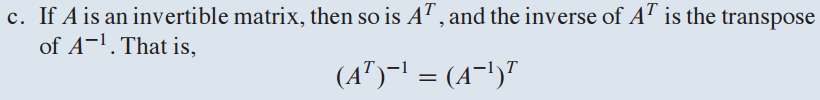
A가 invertible이면 $A^T$도 invertible입니다.
6. 기본 행렬 - Elementary Matrices
기본 행렬(elementary matrix)는 항등 행렬(identity matrix)에 단일 기본 행 연산(row operation)을 적용해서 얻어집니다.

E1은 replacement를 적용한 행렬입니다.
E1A는 A에 replacement를 적용한 것과 동일한 값이 나옵니다.
E2는 interchange를 적용한 행렬입니다.
E3는 scaling을 적용한 행렬입니다.
이를 A와 곱하면 A에도 행 연산을 적용한 결과가 나옵니다.

이것을 가지고 알 수 있는 특성은 다음과 같습니다.
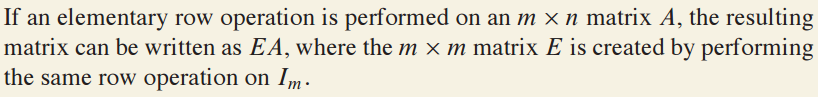
m X n matrix에 elementary row operation을 수행했다는 것은 어떤 m X m elementary matrix가 존재한다는 의미입니다.
A에 적용한 row operation을 m X m indentity matrix에 적용하면 E가 생성됩니다.

elementary matrix E가 invertible이면 E의 inverse는 E를 I로 변환하는 elementary matrix 입니다.

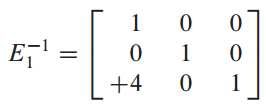
6. 이론 7 - Theorem 7

A가 n X n invertible 행렬이면 A는 $I_n$과 행 상등(row equivalent)합니다.
A를 $I_n$으로 감소시키는 행 연산(row operation)은 $I_n$을 $A^{-1}$로 변환합니다.

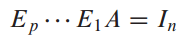


7. $A^{-1}$를 찾는 알고리즘 - Algorithm for Finding $A^{-1}$
A가 m X n 이고 invertible이면 항등 행렬(identity matrix)를 이용해서 $A^{-1}$를 찾을 수 있습니다.

예시
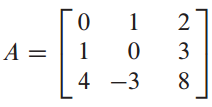

이 방법은 4 X 4부터 굉장히 복잡하여 손으로 구하는건 거의 불가능합니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
