이번 포스팅에서는 선형 변환(Linear Transformation)에 대해 알아보겠습니다.
공부할 내용은 다음과 같습니다.
행렬 곱셈 - Matrix Multiplication
변환 - Transformation
행렬 변환 - matrix transforamtion
선형 변환 - linear transformation
1. 행렬 곱셈 - Matrix Multiplication
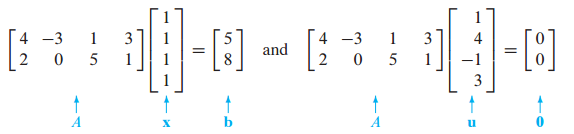
x가 A vector에 의해 b가 되었습니다.
u가 A vector에 의해 0이 되었습니다.

A vector가 $R^4$ space에 있는 x vector를 $R^2$ space로 변환시켰습니다.
이를 변환(Transformation)이라고 합니다.
이처럼 변환(Transformation)은 행렬 곱셈(Matrix Multiplication)에 의해 발생합니다.
2. 변환 - Transformation

$R^n$에서 $R^m$로의 변환(transformation or function or mapping) T는 규칙이 있습니다.
$R^n$에 있는 vector x를 $R^m$에 있는 T(x)로 할당하는 것입니다.
이 규칙을 변환(transformation)이라고 합니다.
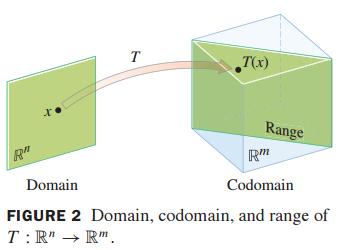
$R^n$ 공간을 정의역(Domain)
$R^m$ 공간을 공역(Codomaion) 이라고 합니다.
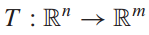
변환은 위 기호처럼 간단히 표현할 수 있습니다.
T(x)를 x의 image라고 합니다.
image의 모든 set을 T의 range라고 합니다.
3. 행렬 변환 - Matrix Transformation
행렬 변환(Matrix Transformation)은 $R^n$공간의 정의역(Domatin)에 있는 x를 $R^m$공간의 공역(Codomation)으로 변환하는 것입니다.
$R^n$공간에 있는 x에 대해서 T(x)는 Ax를 계산하는 것입니다. 여기서 A는 mXn 행렬입니다.
기호로는 아래와 같이 표현할 수 있습니다.


4. 변환 예시
1번 예시



matrix A에서 $x_3$은 0입니다.
$x_3$를 0으로 변환해주므로 기하학적으로 다음과 같이 표현할 수 있습니다.
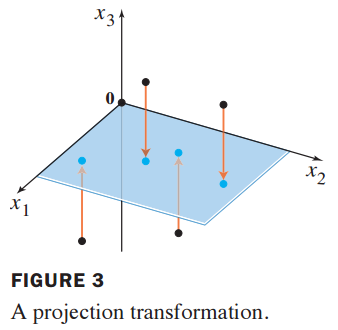
3차원에 있는 임의의 vector에서 $x_3$에 해당하는 value가 zero가 되었습니다.
따라서 Span{$x_1,x_2$} 평면으로 표현되었습니다.
2번 예시
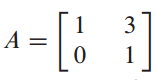

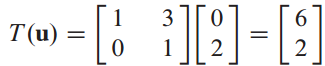
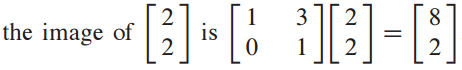

이처럼 변환을 통해 (0,2)과 (2,2)를 (6,2),(8,8)로 변환되었습니다.
이것을 shear transformation이라고 합니다.
5. 선형 변환 - Linear Transformation
변환(Transformation)이 선형 변환(Linear Transformation)이라고 불릴 조건에 대해서 알아보겠습니다.

이 두 가지 조건을 만족하는 Transformation은 linear transformation 입니다.
이는 이전 포스팅에서 공부했었던 Theorem5와 동일합니다.
matrix equation은 linear system이고 이것은 위 두 조건을 성립한다고 배웠습니다.
마찬가지로 위 두 조건을 만족하면 transformation도 linear로 정의가 가능합니다.
mXn matrix가 Theorem5 성질을 지니고 있으므로 모든 matrix transformation은 linear transformation입니다.
linear transformation이 아닌 transformation이 있지만, matrix transformation은 linear transformation 입니다.



linear transformation을 통해 각도가 회전되었습니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
