1장에서 가장 중요한 내용이 선형 독립(Linear Independence) 라고 생각합니다.
이번 포스팅에서 공부할 내용은 다음과 같습니다.
선형 독립(linearly independent)
선형 종속(linearly dependent)
하나의 벡터 집합(sets of one vector)
두 벡터의 집합(sets of two vectiors)
이론 7~9(Theorem 7~9)
1. 선형 독립 - Linearly Independent

$R^n$ 공간에서 vector {$v_1$, ... , $v_p$}가 있을 때 만약 벡터 방정식이 trivial solution(자명해)만 갖고 있을 시에 선형 독립이라고 합니다.
즉, trivial solution만 있으면 linearly independent 입니다.
trivial solution만 존재한다는 의미는 free variable이 없다는 의미입니다.
2. 선형 종속 - Linearly Dependent
벡터 방정식 $c_1v_1 + ... + c_pv_p = 0$에서 weight $c_1, ... , c_p$ 중 하나라도 nonzero면 선형 종속이라고 합니다.
nontrivial solution을 갖고 있으면 최소 1개가 nonzero, 여러개가 zero 일 수 있으므로 linear combination으로 표현되지 않을 수 있습니다.
3. 선형 독립 or 선형 종속 판단 예시 문제
아래 예제에서 선형 독립 or 선형 종속을 판단해보겠습니다.

trivial solution(free variable이 없다)만을 갖고 있으면 linear independent 하므로 augmented matrix로 변환하여 row reduction을 통해 해를 검줄해보겠습니다.
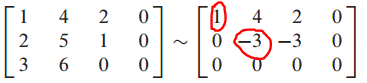
변수는 3개인데 pivot position은 2개 입니다.
이는 free variable이 존재하는 것을 의미합니다.
free variable이 존재하므로 nontrivial solution이 존재하고 해가 무수히 많게 됩니다.
따라서 선형 종속(linear dependent) 합니다.
계속 풀어보겠습니다.


이 vertor set은 linearly dependency 합니다.
하나의 free variable이 존재하여 non trivial solution이 존재하기 때문입니다.
4. 행렬의 열의 선형 독립 - Linear Independence of Matrix Columns

Ax = 0(homogeneous equation)가 trivial solution만을 갖고 있다면 A의 열들은 linearly independent 합니다.
다른 말로 하면 A가 linearly independent하다면 Ax=0은 trivial solution만을 갖고 있습니다.
예시 문제를 한번 보겠습니다.
Ax=0에서 A는 coefficient matrix를 의미합니다.

A의 열들이 linearly independent인지 확인해 보겠습니다.
우선, Ax=0을 augmented matrix로 표현하고 row reduction(행 줄임)을 진행합니다.

모든 row에 pivot position이 있습니다.
이는 free variable이 없다는 것을 의미하므로 trivial solution 밖에 없습니다.
trivial solution 밖에 없으므로 linearly independent 합니다.
5. 하나의 벡터 집합 - Sets of One Vector

집합이 하나의 벡터V만을 갖고 있고 V가 0이 아닐 때 linearly independent 합니다.
V=0이면 $x_1v = x_10 = 0$에서 $x_1$은 임의의 값을 갖게 됩니다.
이는 $x_1$이 free variable을 의미합니다.
따라서 non trivial solution이 존재하게 되어 linearly dependent 하게 됩니다.
V가 0이 아니면 $x_1v=0$에서 0을 만족하려면 $x_1$은 무조건 0이 되어야 합니다.
이는 trivial solution이므로 linearly independent 합니다.
7. 두 개의 벡터 집합 - Sets of Two Vectors

두 vector의 집합에서 하나의 vector가 다른 vector의 scalar multiplation으로 표현 된다면 linearly dependent 합니다.

$v_1 = cv_2$가 $-v_1+cv_2=0$으로 표현된다면 이는 linearly dependent 합니다.
위의 경우에 c는 0이어도 $v_1$의 coefficient는 0이 아니게 됩니다.
$v_1$의 coefficient가 nonzero 하므로 nontrivial solution이 존재하게 되어 linearly dependent가 됩니다.
두 vector의 집합에서 하나의 vector가 다른 vertor의 scalar multiplation으로 표현되지 않는다면 linearly independent 합니다.

vector (3,2)와 vector (6,2)는 scalar multiplation으로 표현되지 않습니다.
이 경우를 linearly independent 하다고 합니다.
8. 두 개의 벡터 집합 예시 문제
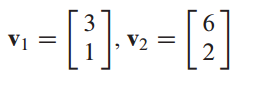
$v_2$는 $v_1$의 scalar multiplation으로 표현됩니다.
따라서 두 벡터는 linearly dependent 합니다
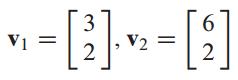
$v_2$는 $v_1$의 scalar multiplation으로 표현되지 않습니다.
따라서 두 벡터는 linearly independent 합니다.
9. 이론 7. 선형 종속 집합의 특성 - Characterization of Linearly Dependent Sets
앞으로 나올 이론7 ~ 이론9는 정말 중요한 이론입니다.
특히 이론7은 나중에 쓰게 되는 곳이 많으므로 꼭 숙지해야 합니다.

집합 S = {$v_1, ... , v_p$}의 두개 이상의 vector가 linearly dependent 하다면 S에 있는 vector들 중 적어도 하나는 다른 vector들의 linear combination으로 표현할 수 있습니다.
다른 말로 하면 최소한 하나의 vector가 다른 vector의 linear combination으로 표현가능하면 2개 이상의 vector는 linearly dependent합니다.
$c_1v_1 + ... + c_pv_p = 0$에서 두 개 이상의 vector가 linearly dependent하다고 가정하겠습니다.
linearly dependent 하므로 하나의 벡터는 다른 벡터의 scalar multiplation으로 표현 가능합니다.
따라서 하나의 vector는 다른 벡터의 linear combination으로 표현될 수 있게 됩니다.
$v_1 = (-c_2/c_1)v_2 + ... + (-c_p/c_1)v_p
만약 S가 linearly dependent하고 $v_1$이 0이 아니라면
$v_j$는 $v_j$이전의 벡터들의 linear combination 입니다.
즉, $v_j$는 $v_j$ 앞에 있는 vector들의 linear combination으로 표현 가능합니다.
여기서 j는 1이 아닙니다.
10. $R^3$ 공간에서의 {u,v,w} - {u,v,w} in $R^3$
u와 v가 linearly independet할 때, set{u,v,w}가 linearly dependet하다면 w는 Span{u,v}입니다.
w is in Span{u,v}의 의미는 Span{u,v}의 solution에 w가 존재한다는 의미입니다.
즉, u와 v의 linear combination으로 w를 표현할 수 있습니다.

S = {u,v,w}가 dependent하면 $v_j$는 $v_{j-1}$의 linear combination으로 표현 가능합니다.
즉 w는 u와 v의 linear combination으로 표현이 가능합니다.
w is in Span{u,v}의 의미입니다.
11. 이론8
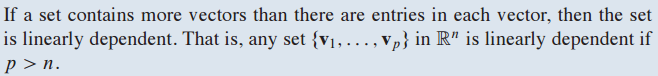
만약 set이 각각의 vector의 entries보다 더 많은 vector을 포함하고 있으면 set은 linearly dependent합니다.

변수는 4개인데 방정식은 3개이므로 free variable을 무조건 갖고 있게 됩니다.
따라서 Ax=0은 nontrivial solution을 갖게 되므로 linearly dependent하게 됩니다.

위 set은 n=2, p=3이므로 1개 이상의 free variable을 갖게 됩니다.
따라서 nontrivial solution을 갖게 되므로 linearly dependent입니다.
위 set을 augmented matrix로 표현하고 row reduction을 진행했을 때 $x_3$에 해당하는 pivot position이 없다는 것을 확인할 수 있습니다.
free variable의 의미는 infinitely many solution을 의미하고 nontrivial solution을 갖게 되며 linearly dependent를 의미합니다.
11. 이론9

set이 zero vector을 포함하고 있으면, set은 linearly dependent합니다.
다른 말로 하면, zero vector을 포함하는 set은 linearly dependent 합니다.

$v_1$을 zero vector로 가정했을 때 $v_2$~$v_p$에 해당하는 coefficient가 0이어도 $v_1$에 해당하는 coefficient는 non zero가 될 수 있습니다.
$v_1$은 0이므로 $c_1$은 어떤 값을 곱해도 0이 성립하기 때문입니다.
nontrivial solution을 갖게되므로 linearly dependent를 의미합니다.
12. 선형 독립 or 선형 종속을 판단하는 예시 문제
1번 문제

p > n이므로 linearly dependent입니다.
하나의 변수가 free variable -> infinitly many solutions -> nontrivial solution -> linearly dependent 때문입니다.
2번 문제

zero vector가 있으므로 linearly dependent합니다.
zero vector의 coefficient는 임의의 값이 되므로 nontrivial solution을 의미합니다.
따라서 linearly dependent 입니다.
3번 문제

linearly independent 입니다.
2개의 vector 중 하나의 vector가 다른 vector의 scalar multiplation으로 표현되지 않기 때문입니다.
이처럼 이론을 숙지하고 있으면 reduced echelon form을 도출해서 solution을 확인하지 않아도 dependency를 빠르게 판단할 수 있습니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
