이번 포스팅에서 공부할 것은 다음과 같습니다.
vectors in $R^n$ : algevraic propreties(대수학적 성질)
linear combination(선형 결합)과 vector equation(벡터 방정식)의 관계
Span{}
1. 2차원 실수체계에서의 벡터 - Vectors in $R^2$
$R^2$가 의미하는 것은 2차원 실수체계를 의미합니다.
벡터의 표현 방법으로는 3가지가 있습니다.
(1) 대괄호

(2) 좌표
u=(3,-1), v=(.2,.3)

(3) 화살표
원점에서부터 vector point까지 화살표를 그려 표현합니다.

2. 벡터 덧셈 - Vector summation
2차원 실수체계 공간에서 두 개의 벡터가 주어졌을 때 덧셈을 할 수 있습니다.

3. 스칼라 곱 - Scalar multiplication
스칼라와 벡터를 곱할 수 있습니다.
스칼라는 단 하나의 값을 의미합니다.
scalar와 vector을 곱하면 vector의 차수를 따르게 됩니다.

4. 2차원 실수체계 공간에서의 기하학적 표현 - Geometric descriptions of $R^2$
벡터를 기하학적으로 표현할 수 있습니다.
(1) 벡터의 덧셈 기하학적 표현


원점에서 vector point까지 화살표를 그리면 됩니다.
(2) 스칼라 곱 기하학적 표현

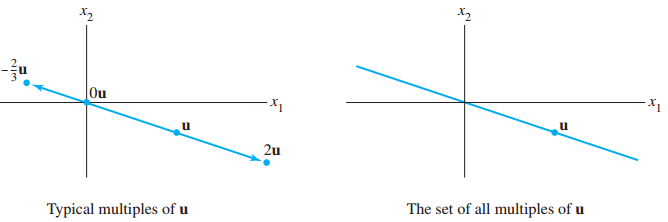
이 의미는 스칼라곱으로 u벡터와 동일선상에 있는 모든 것을 표현할 수 있습니다.
5. 3차원 실수체계에서의 벡터 - Vectors in $R^3$
3차원 공간에서 벡터는 다음과 같이 표현할 수 있습니다.

6. n차원 실수체계 공간에서의 벡터 - Vectors in $R^n$
3차원이 넘어가게 되면 사람이 상상하기가 어렵습니다.
하지만 단순히 $R^n$으로 벡터를 확장하는 것은 쉽습니다.

7. $R^n$공간에서 대수학적 성질 - Algebraic properties of $R^n$

이 성질은 얼핏보면 당연해보이지만 이 8가지 성질이 만족하지 않는 세계도 있습니다.
벡터는 위 8가지 성질을 만족합니다.
8. 선형 결합 - Linear combinations
$R^n$ 공간에서 vector와 scalar가 주어졌을 때 vector Y를 정의할 수 있습니다.
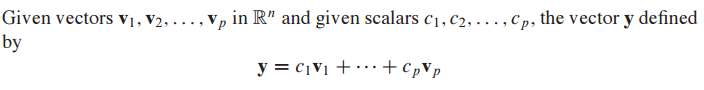
이것을 weights($c_1, ... , c_p$)가 있는 $v_1, ... ,v_p$의 선형 결합(linear combination)이라고 합니다.
weights는 각각의 vector에 곱해진 scalar를 의미합니다.
9. 벡터 방정식은 선형 시스템의 첨가행렬과 같은 해를 갖고 있다.

vector equation과 augmented matrix는 same solution set을 갖고 있습니다.
살펴보겠습니다.

$a_1, a_2, b$가 주어졌을 때 $a_1, a_2$의 선형 결합(linear combination)으로 b를 표현할 수 있습니다.


이제 이 augmented matrix에 row reduction을 이용해 reduced echelon form을 얻고 solution을 도출할 수 있습니다.
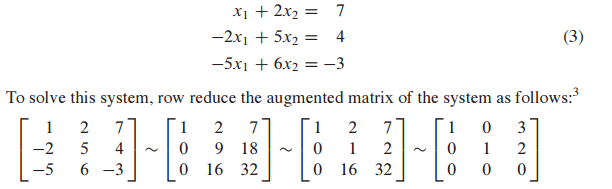
$x_1=3, x_2=2$의 solution을 구했습니다.
10. Span{$v_1, ... ,v_p$}의 의미
$v_1, ... ,v_p$가 있을 때 span은 $c_1v_1 + ... + c_pv_p$ 형태의 linear combination을 의미합니다.
즉, span은 linear combination을 간단히 표현한 것입니다.

11. 3차원 실수 공간에서 Span{v}와 Span{u,v}의 기하학적 표현

Span{v}는 3차원에서 직선
Span{u,v}는 3차원에서 평면으로 나타낼 수 있습니다.
u와 v는 방향이 다른 벡터라는 조건에서 span{u,v}로 표현할 수 있습니다.
12. b가 Span{$a_1, a_2$}에 존재하는지 확인하기
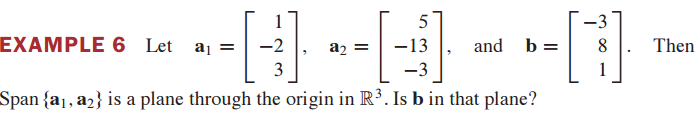
a1, a2, b를 augmented matrix로 표현하고 row reduction을 통해 reduced echelon form을 만들어 solution을 확인해보면 풀 수 있습니다.
augmented matrix로 표현

3번째 방정식이 0=-2입니다.
이는 이론2에 의하면 no solution을 의미합니다.
따라서 b는 span{a1,a2}에 없습니다.
b is not in Span{$a_1, a_2$}
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
