이번 포스팅에서 공부할 것은 다음과 같습니다.
A nonzero row of column (0이 아닌 행과 열)
A leading entry of row (행의 선행 성분)
Echelon form (사다리꼴)
Reduced echelon form (기약 사다리꼴)
Uniqueness of the Reduced Echelon Form (기약 사다리꼴의 유일성)
Row reduction algorithm (행 줄임 알고리즘)
Solution of linear systems (선형 시스템의 해)
일반 해(general soution), 기본 변수(basci variables), 자유 변수(free variable)
Existence and Uniqueness Theorem (유일성과 존재)
이번 포스팅의 핵심은 행 줄임(row reduction)으로 기약 사다리꼴(reduced echelon form)을 얻을 수 있다는 것입니다.
또한 선형 시스템을 기약 사다리꼴로 만든다면 해를 쉽게 찾을 수 있습니다.
1. 0이 아닌 행과 열 - A nonzero row or column
A nonzero row or column은 행과 열의 항목이 1개라도 0이 아닌 것을 의미합니다.
nonzero column
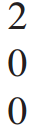
nonzero row
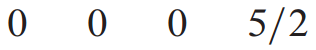
2. 행의 선행성분 - a leading entry of row
A leading entry of row는 행에서 제일 왼쪽에 있는 nonzero entry를 의미합니다.

3. 사다리꼴 - Echelon form
Echelon form은 두 가지 조건을 만족합니다.
(1) 모든 nonzero rows는 all zeros row보다 위에 있다.
(2) 행의 leading entry는 위에 있는 leading entry보다 오른쪽 열에 있다.
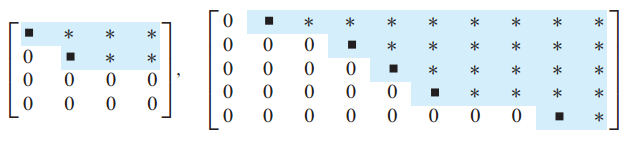
4. 기약 행 사다리꼴 - Reduced echelon form
기약 행 사다리꼴은 사다리꼴의 2가지 조건에서 2가지 조건을 더 만족해야 합니다.
(3) nonzero 행에 있는 leading entry는 1이다.
(4) leading entry가 1인 부분을 제외하고 이것의 열은 모두 0이어야 한다.
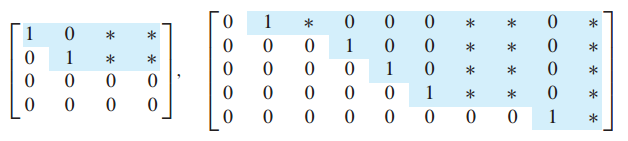
그리고 1의 위치를 pivot position이라고 합니다.
5. 이론1. 기약 사다리꼴의 독특성 - Theorem 1. Uniqueness of the Reduced Echelon Form

각각의 행렬에서 기약 사다리꼴은 1개밖에 없습니다.
다른 형태의 기약 사다리꼴은 없습니다.
6. 행 줄임 알고리즘 - Row reduction algorithm
4단계의 행 줄임(row reduction) 알고리즘을 통해 사다리꼴(echelon form)을 만들 수 있습니다.
그리고 5단계는 기약 행사다리꼴(reduced echelon form)을 만듭니다.
1~4단계를 전향단계(forward phase), 5단계를 후향단계(backward phase)라고 합니다.
전향단계 과정으로 사다리꼴을 만들고, 후향단계 과정으로 기약 행 사다리꼴을 만듭니다.
STEP 1 - 가장 왼쪽의 nonzero 열에서 시작한다. 이곳은 pivot column이며 pivot position이다.

pivot position이 0이므로 다른 행과 interchange를 해줘야 합니다.
STEP 2 - pivot column에서 pivot으로 nonzero entry를 선택해라. 만약 필요하다면 interchange를 해라.

STEP 3 - replacement 연산을 사용해서 pivot 아래의 항목들을 모두 0으로 만들어라

row reduction과정에서 하나의 행렬이 다른 행렬로 바뀌었으므로 이 선형시스템은 행 상등(row equivalent)하다고 할 수 있습니다.
STEP 4 - steps 1-3을 submatrix에 적용해라.



1~4단계인 전향단계(foward phase)를 통해 echelon form이 만들어 졌습니다.
이제 5단계인 후향단계(backfoward phase)를 통해 reduced echelon form을 만들어보겠습니다.
STEP 5 - 맨 아래의 pivot을 1로 만들고 pivot위를 다 0으로 만듭니다.
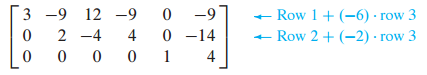



이처럼 5단계를 통해 기약 사다리꼴(reduced ehelon form)을 만들 수 있습니다.
7. 선형 시스템의 해 - Solution of linear systems
첨가행렬(augmented matrix)를 행줄임(row reduction) 알고리즘으로 기약 사다리꼴(reduced ehelon form)을 만든다면 선형 방정식의 해를 쉽게 구할 수 있습니다.
행줄임으로 구한 기약 사다리꼴 형태의 첨가행렬을 보겠습니다.

이를 선형방정식으로 나타낼 수 있습니다.
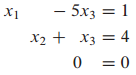
위 선형방정식에서 해를 구하면 다음과 같습니다.

여기서 중요한 것은 일반 해(general soution), 기본 변수(basci variables), 자유 변수(free variable) 용어를 명확히 숙지해야 한다는 것입니다.
(1) 자유 변수 - free variable

$x_3$을 free variable 이라고 합니다.
$x_3$을 어떤 값으로 두어도 0 = 0을 만족하기 때문입니다.
(2) 기본 변수 - basic variables
기본 변수(basic variables)는 자유 변수(free variables)로 표현한 것을 의미합니다.

(3) 일반해 - general solution
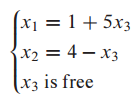
일반 해는 basic variables와 free variables로 표현된 해를 의미합니다.
8. 첨가 행렬에서 일반 해 찾기
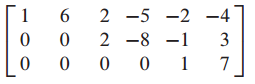
우선 첨가행렬을 행 줄임 과정을 통해 기약 사다리꼴로 만듭니다.

기약 사다리꼴을 선형방정식으로 표현합니다.

일반 해(general solution)은 다음과 같이 표현할 수 있습니다.
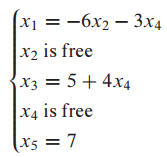
9. 이론2. 유일함과 존재 이론 - Existence and Uniqueness Theorem

이를 해석하면 다음과 같습니다.
(1)
선형 방정식이 consistent이면 augmented matrix에서 b가 pivot position이 아니다.
즉, b를 제외하고 0인 행렬이 있으면 안됩니다.
(2)
선형 시스템이 consistent하면, (i) 자유변수(free variables)가 없다면 해가 1개이다. (ii) 1개 이상의 자유 변수(free variables)가 있다면 해는 무수히 많다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
